Средством, позволяющим адаптировать программную систему под конкретные области человеческой деятельности, является использование шаблонов - готовых иерархий для стандартных задач принятия решений. Под стандартными задачами можно понимать наиболее распространенные задачи ПР, встречающиеся в различных областях человеческой деятельности (например, задачи приведенные в примерах 1 и 2). Используя поставляемые вместе с программой стандартные шаблоны, пользователь может выбрать наиболее подходящий для текущей задачи ПР, загрузить его, подкорректировать в случае необходимости, и приступить к решению своей задачи ПР.

Другое преимущество использования шаблонов заключается в том, что пользователь, работая в той или иной области (например, в медицине, в банковском деле и т. д.), накапливая опыт решения различных задач ПР, может создать свою библиотеку шаблонов, которую потом можно будет использовать другим пользователям, работающим в аналогичных областях.

Библиотеку шаблонов, поставляемую вместе с программой MPRIORITY , планируется периодически расширять (в том числе и за счет шаблонов, полученных от пользователей программы).

Далее рассмотрим возможное применение программной системы для решения задачи оценки эффективности работы персонала фирмы. Причем, предлагаемое ниже решение не ограничено простым созданием соответствующей иерархии, а содержит комплексный подход.

Применение MPRIORITY для оценки работы персонала

Эффективность работы фирмы напрямую связана с эффективностью работы ее персонала. В свою очередь, квалификация персонала фирмы зависит от того, насколько эффективно решаются задачи, связанные с его набором и контролем в процессе функционирования фирмы. Задачу контроля за эффективностью работы персонала фирмы можно представить как задачу ПР, а значит - применить для ее решения MPRIORITY .

Задача Оценка работы персонала фирмы . Пусть у нас имеется n (n < 9) работников. Необходимо ранжировать работников фирмы в порядке уменьшения их значимости для фирмы (в порядке уменьшения эффективности их работы).

Способ 1. Построим для задачи 1 следующую иерархию (рис. 5).

В вершине построенной иерархии располагается цель - оценка работы персонала фирмы. На втором уровне располагаются эксперты. На третьем уровне расположены

возможные в этой ситуации частные критерии: ЧК-1,...,ЧК-8. На четвертом уровне располагается оцениваемый персонал фирмы: Р-1,...,Р-8.

Далее сравнения элементов иерархии будем проводить следующим образом. Объекты второго уровня иерархии на рис. 5 сравнивает руководитель фирмы. По сути, это ни что иное, как делегирование полномочий своим подчиненным (экспертам).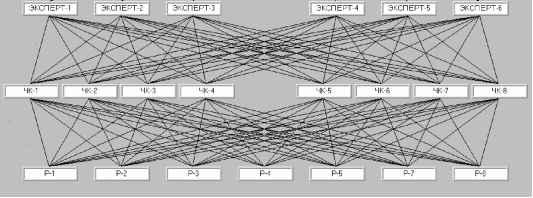

Рис. 5. Иерархия для задачи 1. Обозначим полученный для второго уровня вектор приоритетов через а = {а>1,а>2,...,а>п > (вектор находится в правой части диалогового окна на рис. 6).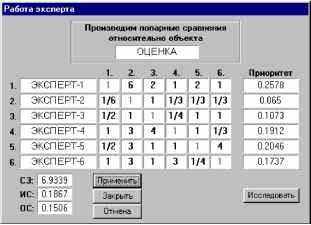

Рис. 6. Парные сравнения, проводимые руководителем фирмы. Объекты третьего уровня иерархии сравнивают эксперты, размещенные на втором уровне (при этом каждый эксперт производит сравнения относительно своего объекта второго уровня - первый эксперт проводит сравнения элементов третьего уровня относительно объекта иерархии Эксперт-1 , второй - относительно объекта иерархии Эксперт-2 и т.д.). Это позволит получить вектор приоритетов для элементов третьего

уровня (этот вектор аккумулирует в себе мнения всех экспертов с учетом веса a>i, i е1: n каждого из экспертов).

Объекты четвертого (нижнего) уровня (относительно всех объектов третьего уровня) поочередно сравнивает каждый из экспертов. После сравнений, проведенных экспертом i, i е 1: n, мы получим вектор приоритетов для объектов нижнего уровня,

отражающий мнение эксперта i. Обозначим этот вектор через р. Пусть все n экспертов провели сравнение объектов нижнего уровня. Сформируем из полученных векторов р, i е 1: n квадратную матрицу Ф размерности n х n (вектора р являются столбцами этой матрицы). Для полученной в этом случае квадратной матрицы Ф и имеющегося вектора со вычислим вектор

ц/ = Фха> .

Полученный вектор приоритетов ц/ ранжирует персонал фирмы с точки зрения его значимости с учетом мнения руководителя фирмы и наиболее влиятельных ее работников (экспертов).

Способ 2. Способ 1 позволяет получить ранжирование персонала фирмы с учетом мнения экспертов и руководителя фирмы. Получим такое же ранжирование, но только с точки зрения оцениваемого персонала (т.е. персонал будет оценивать сам себя). Для этого воспользуемся иерархией, представленной на рис. 5. Применим к этой иерархии схему попарных сравнений, аналогичную схеме в способе 1 за одним исключением: объекты четвертого уровня будут поочередно сравнивать не эксперты, а персонал. После сравнений, проведенных сотрудником i, i е 1: n, мы получим вектор приоритетов р объектов нижнего уровня, отражающий мнение сотрудника i (в этом случае будет интересно посмотреть, какой вес приписывает сотрудник фирмы сам себе относительно своего коллектива, т. е. выяснить его самомнение ). Далее вычислим вектор

ц/ = Фхсо,

где Ф (как и в способе 1) - квадратная матрица размерности n х n, сформированная из векторов р ,i е 1: n, со = (1/n,1/n,к,1/n) (сотрудники имеют равные веса, т. к. на данном этапе у нас нет достаточных оснований отдавать предпочтение тому или иному сотруднику). Полученный вектор приоритетов ц ранжирует персонал фирмы с учетом мнения самого персонала фирмы.

Способ 3. Получим ранжирование персонала фирмы с точки зрения самого персонала, но исключим при этом из вектора щ самомнение каждого из сотрудников. Для этого сотруднику i, i е 1: п предоставим иерархию, аналогичную иерархии на рис. 5, за следующим исключением: из самого нижнего уровня удалим элемент, соответствующий сотруднику i (чтобы не дать сотруднику i сравнить самого себя с остальными сотрудниками).

Сравнения элементов второго и третьего уровня иерархии для сотрудника i соответствуют сравнениям иерархии из способа 2.

Пусть 51 - вектор приоритетов объектов нижнего уровня размерности п -1, полученный после сравнения элементов четвертого уровня сотрудником i . Сформируем из вектора 51, вектор р размерности п путем добавления в вектор 51 на позицию i нулевого элемента. Как и в способе 2 из векторов р, i е 1: п составим квадратную матрицу Ф размерности п х п (вектора р являются столбцами этой матрицы, таким образом, на главной диагонали матрицы Ф будут стоять нулевые элементы). Вычислим вектор

щ' = Фхса,

где со = (1/ п,1/ п,... ,1/ п>.

Полученный вектор щ (как и в способе 2) ранжирует персонал фирмы, но в отличие от вектора щ не содержит в себе мнение i -го сотрудника относительно себя.

После проведенных парных сравнений способами 1-3 мы получили три вектора щ', щ , щ . Теоретически, соответствующие значения всех трех векторов должны совпадать.

На практике же вектора могут иметь (можно даже сказать, что в большинстве случаев они будут иметь) отклонения друг от друга (именно по этой причине парные сравнения и были проведены тремя способами). Таким образом, анализ руководителем фирмы полученных векторов с учетом остальной полученной информации (такой, как согласованность матриц парных сравнений, собственные вектора этих матриц) может оказаться для него весьма интересным и информативным.

Один из возможных вариантов анализа полученных векторов щ ,щ , щ заключается в применении к ним метрики, введенной в работе [1]. Переходя на терминологию Дж. Кемени, вектора приоритетов, ранжирующие объекты (например, персонал фирмы), будем называть упорядочениями (упорядочениями будут являться

полученные ранее вектора ц , ц , ц , если элементы векторов (веса) отсортировать в порядке убывания и заменить веса наименованиями объектов, которым этот вес принадлежит).

Предположим, что несколько экспертов упорядочивают по предпочтениям множество объектов (под экспертами в нашем случае можно понимать использование в диалоговом режиме программы MPRIORITY , а под объектами - персонал фирмы). Таким образом, мы имеем несколько векторов (упорядочений).

Необходимо:

1) определить, насколько близки ( далеки ) два различных упорядочения экспертов (в нашем случае это позволит выяснить, насколько близки мнения руководителя фирмы, экспертов и самого персонала);

2) найти такой вектор (назовем его согласующим), который в каком-то смысле наилучшим образом согласуется со всеми упорядочениями экспертов.

Для того чтобы выполнить перечисленные выше пункты 1 и 2, следует превратить множество всех возможных упорядочений в некоторое геометрическое пространство. В этом пространстве можно как подсчитать расстояние между двумя любыми упорядочениями, так и найти согласующий вектор [1] (любое упорядочение будет являться точкой этого пространства). Дж. Кемени на базе четырех аксиом строит такое геометрическое пространство и определяет в нем расстояние между двумя любыми упорядочениями.

Определим далее матрицу упорядочений n объектов (объекты будем обозначать маленькими латинскими буквами).

Квадратная матрица A размерности n х n, элементы которой aij, i, j е 1: n

определены следующим образом:

1, если объект i предпочтительнее объекта j, aiJ =<-1, если объект j предпочтительнее объекта i, 0, если объекты i и j равноценны,

называется матрицей упорядочений n объектов.

Таким образом, для любого упорядочения эксперта можно построить соответствующую матрицу A. Далее, пусть т1 и т2 - два упорядочения, а A и A две соответствующие им матрицы предпочтений, тогда расстояние между упорядочениями т1 и т2 определяется по следующей формуле:

d(T1,T2) = 2 Z \ a l - a \,

где aj и a - элементы матриц упорядочений A и A соответственно.

Замечание 1. Минимально возможное положительное расстояние между двумя предпочтениями равно 1.

Замечание 2. Максимально возможное расстояние между упорядочениями из п объектов равно 2п.

Таким образом, получив вектора щ ,щ и щ, можно подсчитать расстояние между ними и, с учетом замечаний 1 и 2, понять, насколько близки (далеки) мнения: руководителя фирмы, экспертов и персонала.

Заметим, что расстояние Кемени между суждениями экспертов не является единственно возможным (следует также заметить, что это расстояние учитывает только позицию объекта в векторе приоритетов, и не учитывает вес объекта). Поэтому вполне возможно применение других способов и подходов, позволяющих вычислить близость векторов щ ,щ и щ .

Для определения согласующего вектора (пункт 2) введем следующие необходимые понятия. Пусть т1 ...тт - упорядочения (точки геометрического пространства), полученные различными экспертами. Тогда точка

Tmed = min Z d(Ti ,Tmed )

ie1:m

называется медианой множества точек т1 ...тт, а точка

Ттеап = П Z d(Т ,Ттеап )2

ie1:m

является средним значением множества точек т1 ...Tm .

Таким образом, подсчитав для векторов щ ,щ и щ величины Tmed и т1пеап, можно

определить их согласующий вектор.

Сделаем несколько полезных замечаний относительно медианы и среднего значения [1].

1. Медиана и среднее значение определяют согласованные упорядочения для множества исходных упорядочений различных экспертов.

2. Медиана учитывает мнение большинства экспертов, тогда как среднее значение может посчитать преимущество большинства не вполне убедительным и тем самым провозгласить равноценность.

3. Среднее значение всегда единственно, тогда как медиан может от одной до m , где m - количество экспертов(упорядочений).

Заключение

В работе предложено и описано средство, позволяющее достаточно оперативно и эффективно решать различные задачи ПР, возникающие в различных областях человеческой деятельности.

Как показано в статье, к данным, полученным при помощи программной системы MPRIORITY , возможно применение дополнительных методов (например, статистических), позволяющих расширить количество возможных выводов.

Литература

1. Кемени Дж., Дж. Снелл Кибернетическое моделирование. - М.: Советское радио, 1972, 192 c.

2. Миллер Г. Магическое число семь плюс или минус два. О некоторых пределах нашей способности перерабатывать информацию. Инженерная психология. - М.: Прогресс, 1964, - C. 192-225.

3. Саати Т. Принятие решений. Метод анализа иерархий. - М.: Радио и связь, 1993, 316 с.