Об идентификации математической модели развития эпизоотии

Слиденко А.М., Соловьева Т.Е., Кромина М.А. (magdalena.vrn@mail.ru)

Воронежский государственный аграрный университет им. К.Д.Глинки

Изучению процессов распространения инфекционных заболеваний посвящены работы ряда авторов ([1]-[3]). Применение метода математического моделирования с развитием вычислительной техники становится все более эффективным. Особенности конкретного заболевания конкретизируют математическую модель. Проверка согласованности модели с опытными данными в каждом случае имеет решающее значение.

В данной работе рассматривается модель распространения лейкоза в изолированной группе животных. Наличие опытных данных позволяет сформулировать задачу идентификации и найти одно из ее решений. При этом используется система программирования Mathcad.

Среди болезней сельскохозяйственных животных лейкоз занимает существенное место. Это заболевание не только приводит к гибели и преждевременной выбраковке животных, но и ставит под угрозу развитие племенных хозяйств, снижает эффективность селекционной работы и использование продуктов животноводства. В настоящее время признано, что заболевание имеет инфекционную природу, а его этиологическим фактором является вирус ВЛКРС (вирус лейкоза крупного рогатого скота). Изучение процесса заболевания в изолированной группе животных является актуальным, так как для борьбы с ним необходимо уметь прогнозировать протекание болезни.

Рассматривается большая изолированная группа животных (стадо), состоящая из N животных. В этой группе распространяется инфекционное заболевание - лейкоз. Отметим характерные особенности данного заболевания.

1. Наличие незначительного инкубационного периода.

Рис.1. Возможные состояния животных Следует отметить, что в данном случае предполагаются переходы: Y - R, Y - S, G - R. Возможность таких переходов допускается в связи с искусственным введением в стадо здоровых животных и выведением из стада больных и инфицированных особей. При этом нет эмпирических данных относительно количественных характеристик таких процессов. Кроме того, предполагается малая вероятность таких переходов при данном заболевании.

2. Наличие длительной латентной стадии (промежуток времени от заражения до проявления клинико-гематологических признаков).

3. После заражения вирусом животное может служить источником передачи инфекции даже через несколько дней после инфицирования. Предполагается, что все стадо состоит из четырех групп животных,

организм которых находится в различном состоянии относительно данного заболевания.

1. Сенсибильные (восприимчивые) животные. Их число зависит от времени: S = S (t);

2. Инфицированные животные, обозначим их число через Y = Y (t);

3. Больные животные (животные, находящиеся в гематологической стадии заболевания), число таких животных обозначим G = G(t);

4. Резистентные (устойчивые к данному заболеванию), их число в момент времени t равно R = R(t).

Характер и особенности заболевания определяют возможности переходов животных из одной группы в другую по схеме, представленной на рис.1.

= а- S (t) -p- Y (t -11) -y- Y (t)-S-Y (t),

- = -а- S (t) + S- Y (t) + p1 - G(t -12), dt

dG = p- Y (t -11)-P1 - G(t -12), dt

= У- Y (t).

(1.1)

В любой момент времени t справедливо равенство N = Y (t) + S (t) + G (t) + R(t), (1.2)

где N = const.

Задавая начальные условия Y(t) = Yo,S(t) = So,G(t) = Go,R(t) = Ro, t e [0;l], (1.3)

где l = max{/1, 12}, приходим к начальной задаче (1.1) - (1.3).

Применение этой модели предусматривает использование таких важнейших параметров как показатель а и в , характеризующих тяжесть эпизоотической ситуации. Эти величины зависят от уровня инфицированности

Относительно интенсивностей таких переходов сделаны следующие предположения.

Скорость перехода S - Y в момент времени t пропорциональна числу сенсибильных животных в тот же момент времени. Скорость обратного перехода пропорциональна числу инфицированных особей. Интенсивность перехода Y - G в некоторый момент времени t пропорциональна числу инфицированных животных в более ранний момент времени t -11. Скорость

перехода Y - R пропорциональна общему числу инфицированных животных.

В связи с проведением гематологических исследований на лейкоз через 6 месяцев и реже, предполагается, что выбраковка больных животных G - S осуществляется с некоторым запаздыванием l2, ее интенсивность пропорциональна числу больных животных в момент времени t -12.

В результате сделанных предположений, с учетом уравнений баланса, получена система дифференциально-разностных уравнений dY

и характеризуют интенсивность распространения инфекции и заболеваемости среди животных этого стада. Коэффициенты а и в являются параметрами, описывающими естественный ход эпизоотического процесса.

Вторым уровнем, отображаемым в модели, являются социально-экономические факторы, к которым причислены ввод здоровых особей, выбраковка инфицированных и больных животных. Основными показателями выбраковки и ввода животных являются коэффициенты 8 и р1 соответственно.

Коэффициент у характеризует количество особей, имеющих устойчивость к данному заболеванию.

Рассмотрим случай, когда параметры /1 и 12 принимают постоянные

значения: /1 = 1; / 2 = 1.

Обозначим через a = {а, Р,у,8, /1} точку в пятимерном пространстве, координатами которой являются параметры модели. Пусть Y (tk, a)- решение начальной задачи (1.1) - (1.3) (число инфицированных животных в момент времени tk), Y*k - опытные значения Y, к=1,2,... ,m, где m - число измерений.

Введем функцию

U(a) = Х (Y(tk, a) - Yt )2. (1.4)

Функция (1.4) характеризует близость опытных и модельных значений Y. Точка a является аргументом этой функции, так как Y(tk,a) зависит от a.

Необходимо найти значение вектора a, которое минимизирует функцию U(a)

при условии

a > 0 (1.5)

Пусть

gradU = VU

dU dU dU dU dU *

VTU (а)

dadpdydS dp1 J - градиент функции U(a), AaU ApU AyU ASU Ap1U

разностный аналог

T T T T T

градиента функции. Здесь частные производные первого порядка аппроксимируются разностными отношениями с первым порядком относительно t , т.е.

dU U(а + т,p,...,p1)-U(a,p,...,p1) = AaU

- rsj - - -

да т т

dU U(а,p...,p1 +t)-U(а,p,...,p) = Ap1U

- rsj - - -

dp1 т т

Обозначим через a(p+l1 и a(p) приближения a в итерационном процессе

а(p+1) =а(p) - h -VU(а(p)). (1.6)

Здесь h - параметр итерационного процесса, который выбирается определенным образом. В обычном градиентном методе он выбирается опытным путем. От выбора h зависит эффективность и экономичность метода. Итерационный процесс продолжается до выполнения условия

U(а(p))-U(а(p<£, (1.7)

Блок - схема программы в этом случае представлены на рис.2.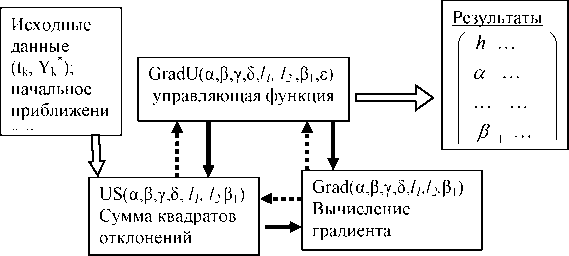

, и ,

Du(a,P,Y,8,/i,/2 P1) Решение начальной задачи численным методом

Рис. 2. Блок - схема программы. На схеме приняты следующие обозначения:

вызов функции; передача результатов вычислений;

1 передача исходных данных и окончательных результатов.

Для построения математической модели использованы экспериментальные данные по молочному поголовью ОПХ за десятилетний промежуток времени.

На рис. 3 представлены расчетные Y(t), G(t) и экспериментальные

(Jl, tk) кривые. Расчетные кривые получены при начальном значении вектора а={0,08; 0,1; 0,01; 0,015;0,01}. При этом параметры li=l2=1. Все эти параметры

задают начальное приближение метода градиентного спуска и выбираются с

помощью предварительных вычислений.

0 20 40 60 SO 100 120 140

Рис. 3. Начальное приближение Далее осуществлялась процедура градиентного спуска. Результат итерационного процесса представлен на рис. 4.

о

о ::i 40 ба зо 100 120 no

Рис. 4. Результат градиентного спуска Значения параметров математической модели вычислялись на каждом шаге итерационного процесса. Изменения параметров представлены на рис.5.

Т 0.05 Б О

О 2 4 6 8 10 12 14 16 IS 20 22 24 26 28 30

Рис. 5. Изменение параметров модели в итерационном процессе После осуществления процедуры градиентного спуска зависимости Y (t) и

G(t) приведены на рис.4. При этом вычислены значения неизвестных

коэффициентов: а = 0,097 0 =0,041 у=0,019 5=0,012 01=0,254.

Следует отметить, что предложенная модель прогнозирует только главную тенденцию развития эпизоотии. Поэтому целесообразно рассматривать изменение по времени относительных переменных, характеризующих долю животных, находящихся в определенных состояниях. Такие графики приведены на рис. 6.

0 20 40 60 80 100 120 140

Рис. 6. Относительные переменные: y = Y, s = S, r = R, g = G.

N N N N

Коэффициент а характеризует скорость перехода восприимчивых животных в инфицированные, а в - скорость перехода инфицированных в больные. Зная значения для этих показателей, мы сделали вывод, что интенсивность инфицирования особей на опытной станции ВГАУ превышала заболеваемость в два раза.

Коэффициенты второго - социально-экономического уровня 8 и р1 характеризуют выбраковку РИД (+) животных и больных соответственно. Интенсивность скорости выбраковки больных в два раза превышает интенсивность выбраковки инфицированных.

Устойчивость коров к лейкозу в стаде опытной станции ВГАУ очень низкая и составляет около 1,9% от всех подвергшихся заражению вирусом животных в единицу времени.

Анализируя построенную модель, можно сделать вывод о том, что хотя выбраковка коров на опытной станции ВГАУ не имела четкой тенденции и проводилась по мере возможности, на рис.4 отчетливо видно снижение количества инфицированных голов.

Сопоставление результатов расчета и наблюдений позволяет сделать вывод о непротиворечивости математической модели.

0.8 0.64

s 0.48

I 0.32

----0.16

Литература

1. Гулюкин М.И., Замараева Н.В., Коромыслов Г.Ф. Лейкоз крупного рогатого скота - одна из важнейших проблем ветеринарии. Ветеринарная газета. - 2001. - №5. - С. 1-2.

2. Т.Е. Соловьева, А.М. Вислогузов, Ю.А. Каган. Эпизоотологическая ситуация по лейкозу крупного рогатого скота в Воронежской области. Теория и практика научного развития АПК.- Воронеж, 2003. - С. 96-99.

3. Таршис М.Г., Константинов В.М. Математические методы в эпизоотологии. - Москва,1975.-170 с.

Заключение

1. Построена модель с учетом запаздывания, представляющая систему дифференциально-разностных уравнений.

2. Для идентификации модели разработан алгоритм, использующий разностный аналог градиентного метода первого порядка аппроксимации.