Об уравнениях движения вязкого газа

Ракогон Ю.Г. (khan@ptci.ru)

Московский физико-технический институт (государственный университет)

1. В МФТИ проводились экспериментальные исследования внутренних ламинарных течений вязкого газа в цилиндрических воздухозаборниках и круглых трубах с дозвуковыми скоростями во входных сечениях в условиях, когда еще выполняется гипотеза сплошности среды [1]. Исследования показали, что взаимное влияние вязкости и сжимаемости приводит к такому искривлению линий тока, что газ внутри канала, вблизи выходного сечения, разгоняется до сверхзвуковых скоростей. В связи с переходом через скорость звука нормальная составляющая скорости v меняет знак и возникает своеобразный эффект отражения газа от оси симметрии. Этот эффект по своему действию противоположен вытеснению газа от стенки из-за вязкости. По видимому, при внешнем давлении, стремящемся к нулю, звуковая линия асимптотически приближается к стенке канала. Качественная картина течения приведена на рисунке.

В поле течения, в зависимости от поведения плотности тока газа pV вдоль линий тока, можно выделить следующие характерные области:

область I, в которой д (pV)/dl < 0 (dl - элемент дуги линии тока), область II, в которой d(pV)/dl > 0,

сверхзвуковая область Ш,где так же, как и в области I, d(pV )/dl < 0.

Внутри области I существует также область, примыкающая к стенке, где газ тормозится. Максимальные значения pV на звуковой линии достигаются при изоэнтропичности перехода через скорость звука.

Вдоль всех линий тока энтропия S растет, достигает максимального значения при скорости равной скорости звука и сохраняется вдоль линий тока сверхзвуковой области.

При истечении в вакуум внутреннее течение на звуковой линии изолируется от внешних условий. И, таким образом, адиабатическое течение в трубе будет необратимым процессом в изолированной системе, ограниченной стенками трубы и звуковой линией.

Предполагаемый характер течения не противоречит законам сохранения и второму началу термодинамики, но не согласуется с уравнениями Навье-Стокса, не допускающими существования таких областей течения, где диссипация механической энергии отсутствует, если в потоке имеются деформации жидких элементов.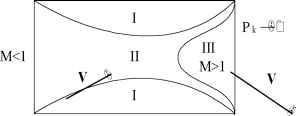

2. Уравнения Навье-Стокса для сжимаемого газа не достаточно универсальны в том смысле, что они не допускают непрерывного перехода в уравнения Эйлера. Поэтому, широкое распространение получили приближенные подходы, состоящие в искусственном разделении течения на пограничный слой около стенки, где влияние вязкости существенно, и невязкое течение в остальной области. В соответствии с этим подходом около стенки решаются уравнения пограничного слоя Прандтля, решения которых затем сращиваются с решениями невязких уравнений Эйлера.

Другим подходом является применение метода асимптотических разложений, когда число Рейнольдса устремляется в бесконечность, и на большей части течения влияние вязкости исчезает, а уравнения Навье-Стокса заменяются уравнениями Эйлера.

В настоящей работе предпринята попытка видоизменить уравнения Навье-Стокса, чтобы они допускали непрерывный переход в уравнения Эйлера, когда объемные вязкие силы обращаются в нуль при конечном значении числа Рейнольдса. Повидимому, если такой переход возможен, то он должен осуществляться на звуковой линии, разделяющей вязкое дозвуковое и невязкое сверхзвуковое течения .

В работе используется подход Л.Д.Ландау [2], считавшего, что для установления уравнений движения вязкого газа необходимо добавить к правым частям уравнений Эйлера объемные силы, зависящие от вязкости.

3. Среди всех допущений, лежащих в основе вывода уравнений Навье-Стокса движения вязкого сжимаемого газа (изотропность сплошной среды, инвариантность при вращении системы координат, линейная связь напряжений со скоростями деформаций), наименее убедительной представляется гипотеза Стокса о связи между коэффициентами вязкости: 3Л + 2ц = 0, где j - коэффициент вязкости деформаций сдвига, а Л - коэффициент объемной вязкости. В соответствии с этой гипотезой связь тензора напряжений с тензором скоростей

ды, ды, 2 ды,

деформаций имеет вид: Tik = ц

\dxk дХг 3 дХ1 J

По существу,

соотношение Стокса искусственно приводит к равенству нулю линейного инварианта тензора напряжений, как это имеет место в несжимаемой жидкости , тем самым, в уравнения движения могут быть привнесены некоторые свойства несжимаемости среды.

Сомнения о справедливости гипотезы Стокса выражали многие механики. Приведем высказывание Дж.Серрина [3] по этому поводу: Аргументация Стокса в настоящее время кажется неубедительной; правда и сам Стокс позднее указывал, что он никогда не был полностью уверен в справедливости этого соотношения. Что касается кинетической теории Максвелла, то, как показал Трусделл, в ее основе лежит предположение равносильное соотношению 3Л + 2 j = 0.

Попытаемся определить связь Л(ц) из условия изоэнтропичности перехода

через скорость звука на линии тока (ось x), совпадающей с плоскостью симметрии произвольного сверхзвукового сопла. Учитывая, что вдоль линии тока (благодаря

. du dv

симметрии) нормальная компонента скорости v и производные - и - равны

dy dx

нулю, запишем систему уравнений: Навье-Стокса вдоль оси x, неразрывности и выражения для производной давления P как функции двух переменных плотности

du 1 dP dTxx dTyx

p и энтропии S

du dv u dp dP

- + - +--- = 0, -

dx dy p dx dx

dx p dx dx dy

f dP dp :f dP ) dS dx

KdpJs

dS Jp dx

f dP

\dpJ S

- квадрат местной скорости звука.

При M = 1 - и вязкая часть уравнения Навье-Стокса равны нулю, и, разрешая

dv dv

эту систему относительно производной -, получим: -

dy dy

M =1

pu dx

То есть, при M = 1 производная

dv dy

- 0. Рассмотрев далее выражение для

диссипации механической энергии E в общем виде, окончательно будем иметь:

(2/1 + Л)

Поскольку производная

du dx

кривизне звуковой линии, например, [4], то

du dx

пропорциональна

> 0. Для отсутствия

диссипации механической энергии при переходе через скорость звука необходимо принять: Л = -2/и.

К такому же результату приводит и другое рассуждение. Рассмотрим выражение для нормального вязкого напряжения в несжимаемой жидкости,

например, Txx. Поскольку divV = 0, то Txx = 2 - = -2

fdv + dw dy dz

Это

очевидное равенство позволяет по-разному толковать, как зависит нормальное напряжение от скоростей деформаций. С одной стороны, оно пропорционально

скорости удлинения элемента жидкости -, а, с другой стороны, - скорости

нормальной направлению напряжения. Если

( dv dw

изменения площади

dy dz

предположить, что в газе, также как и в жидкости, нормальные вязкие напряжения пропорциональны скоростям изменения площадей перпендикулярных направлениям напряжений, то будем иметь, например:

~ du I

du dv dw

- + - +-

dx dy dz

dv dw +

dy dz

M =1

Таким образом, получаем, что A = -2(i.

4. Тогда связь напряжений со скоростями деформаций будет:

f ды i ды.

дх1 J

А уравнения движения вязкого газа приобретут вид:

р

ды i ды.

2*k £Л

дх1 J

В соответствии с (2) правые части (зависящие от вязкости) будут:

F 2 д (ду Fx =-2-( -

дх уду

д

- М

дм Л ды Л

д f ду дх

д f ды

Если положить,

что

дх J ду ( = const

д f дм ды 2-(I - + -

ду удz дх

ду Л дz

д f ды (I

д f ды 2(

+ дУ дz J

то после

простых преобразований проекции

объемных вязких сил (3) могут быть представлены в виде :

д

(Ау - (-divV, Fz = (А

д

Aw - (-

divV.

Отсюда следует, что вектор объемной вязкой силы будет зависеть только завихренности: F = (AV - (graddivV = -(rotrotV, (5)

а уравнения движения вязкого газа (2) могут быть сведены к обобщенному уравнению Гельмгольца, например [5], для вязкой несжимаемой жидкости, которое представляет собой уравнение переноса и диффузии вихрей вследствие трения.

Функцию диссипации E механической энергии в соответствии с тензором скоростей деформации (1) нельзя выразить в виде суммы квадратов элементов скоростей деформаций, но можно представить как сумму квадрата вихря вектора скорости и якобианов скоростей в следующем виде:

f ду ды ды ду Л fды дм ды дм Л (дм ду ду дм Л

E = ((rotV) + 4(

дх дудхду

дz дх дх дz

ду дz ду дz

Заметим, что выражение (6) совпадает с выражением диссипации механической энергии в несжимаемой жидкости:

E = (

fду дх

ды Л ду

: ((rotV)2 + 4(

ду ды дхду

дм Л

ды дм дz дх

-4(1

ды ду дхду

ды дм дх дz

ду Уду J

Ik J

дм + дуЛ

дмдуЛ ду дz у

Если считать, как в динамике идеального газа, что в дозвуковой области якобианы положительны и не могут менять знак, например [6], то выражение (6) не может быть отрицательным при M < 1. Если же завихренность исчезает, то течение становится потенциальным, уравнения (2) обращаются в уравнения Эйлера и

дудмЛ ду дz

понятие диссипации энергии вследствие вязкости теряет смысл. Однако неотрицательность функции E в вязком газе требует специального рассмотрения.

5. Дж.Бэтчелор [7] обращал внимание на противоречие, которое он считал кажущимся, что в несжимаемой жидкости при постоянной вязкости, с одной стороны, напряжения возникают вследствие деформаций и не зависят от локальной завихренности, но, с другой стороны, что результирующая сила вязкости на единицу объема пропорциональна производной от завихренности по координатам.

Отмеченная Бэтчелором особенность не является противоречием, она имеет место и в газе: как было показано объемная вязкая сила уравнений (2) при М = const также может зависеть только от завихренности (5). Эта особенность -следствие возможной двойственности описания динамики жидкости и газа: с одной стороны, - уравнение Навье-Стокса, основанное на связи вязких напряжений с симметричным тензором скоростей деформаций, с другой стороны - обобщенное уравнение Гельмгольца диффузии завихренности. Возможность различной интерпретации динамики жидкости следует из простого примера течения между двумя параллельными плоскостями. Такое течение является не только сдвиговым, но и завихренным, поэтому напряжение трения может быть выражено не только

через деформацию сдвига, но и через rotV :

-U ( rotV ) = U-.

Поскольку практически все вязкие течения характеризуются возникновением и диффузией завихренности, то возникает вопрос: нельзя ли установить уравнения движения вязкого газа, используя связь напряжений только с антисимметричным

тензором скоростей деформаций:

ди ди,

\дхк

Для ответа на этот вопрос рассмотрим выражения (4) проекций вязких сил уравнения (2). После несложных преобразований выражения (4) можно представить в другом тождественном виде:

д f ду

д f ду дх

Fz =-М

дм \ д f дм?

д f ди

дх удг дх j ду У ду

Заметим, что такое же выражение сил может быть получено из уравнений Навье-Стокса и для несжимаемой жидкости. Из (7) следует:

1. входящие в проекции сил компоненты rotV являются удвоенными элементами антисимметричного тензора скоростей деформаций;

2. нормальные составляющие сил отсутствуют.

Если считать, что напряжения, возникающие в движущемся газе, зависят только от завихренности, то получим:

дх, дх.

тензор касательных напряжений.

Тогда уравнения движения приобретут простой вид

р

диссипация

E = 2(A2 = 2(

механической

ды, ды.

J

энергии

ды дм V + 1 дz дх J 2

будет

выражаться

через rotV

((rotV )2

(10)

Заметим, при постоянной вязкости уравнения (2) и (9) совпадают и различие обоих подходов проявляется только в функциях диссипации механической энергии (6) и (10). В соответствии с выражением (10) вязкие напряжения в движущейся среде не возникают в случаях, когда течение становится безвихревым и, следовательно потенциальным, а уравнения движения обращаются в уравнения Эйлера. В отличие от движений вязкой несжимаемой жидкости, в которых диффузия завихренности завершается только асимптотически, например [6], в вязком газе завихренность может исчезать на звуковой линии. И, таким образом, звуковая линия будет геометрическим местом точек, в которых не только M = 1, но и rotV = 0.

Использование аксиоматики, основанной на связи напряжений с антисимметричной частью тензора скоростей деформаций, позволило установить уравнения движения вязкого газа (9). Эти уравнения отражают, в частности, тот факт, что вязкость проявляется в движущейся среде не одномерным образом. Поэтому, нормальные напряжения равны нулю (тТ = 0), и дивергенция скорости не

входит в уравнения. (Исключением могут быть такие движения, когда необходимо привлекать вторую вязкость [2]).

Двойственность описания динамики жидкости и газа может быть исключена, если принять, что в движущейся вязкой среде имеют место только касательные напряжения, зависящие от антисимметричной части тензора скоростей деформаций.

Находит новое обоснование граничное условие равенства нулю тангенциальной скорости на стенке. Выделенный в газе цилиндр, касающийся стенки, под действием касательных сил трения качения как бы катится по стенке. Мгновенная ось вращения проходит через точку касания цилиндра со стенкой и скорость этой точки (как следует из динамики твёрдого тела) равна нулю.

Литература

Аэрофизика и прикладная математика ,

1.Ракогон Ю.Г., Труды МФТИ. Серия часть I, 1975.

2.Ландау Л.Д., Лифшиц Е.М. Механика сплошных сред. М., 1953. З.Серрин Дж. Математические основы классической механики жидкости. М., 1963. 4. Овсянников Л.В. Лекции по основам газовой динамики. М. Наука, 1981. 5.Лойцянский Л.Г. Механика жидкости и газа. М., 1957.

6.Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика М., 1953. 7.Бэтчелор Дж. Введение в динамику жидкости. М., 1973

а