Электропроводность, характеристики носителей тока, диэлектрическая проницаемость и структура растворов

электролитов. II. Эффективная масса носителей тока и плазменные

колебания

Фенин А.А. (fmkfenin@rctu.ru), Фенин С.А., Ермаков В.И. Российский Химико-технологический университет им. Д.И. Менделеева

Введение

В работе [1] нами рассмотрен метод определения электрических характеристик растворов электролитов с использованием бесконтактных измерительных ячеек и способ расчета искомых электропроводности (ЭП) и диэлектрической проницаемости (ДП) путем выделения составляющих импеданса измерительной ячейки с исследуемым раствором. Приведены результаты измерения ЭП водных растворов KCl в интервале концентраций 10-5 - 10-3 м/л и при температурах 18-29°C, которые сопоставлены со справочными данными, выполнен методологический анализ проведенных измерений. В настоящей работе рассматривается физико-химическая сторона обсуждаемого вопроса и анализируется возможность плазменных колебаний в растворах электролитов.

Физико-химический аспект. Перестройки структуры в растворах электролитов при изменении их концентрации

Рассмотрим зависимость удельной ЭП исследованных растворов от их концентрации и температуры [1, табл.3]. Как следует из рис.1, построенного по данным этой таблицы, удельная ЭП водных растворов KCl в интервале концентраций 110-5 - 110-3 м/л изменяется практически линейно с коэффициентами корреляции 0.99991 для t = 18oC и 0.999888 для t = 29oC. Отсюда следует два существенных вывода.

Рис.1. Зависимость удельной ЭП водных растворов KCl от их концентрации в интервале 1.10-5 -1.10-3 м/л при t = 18oC удельная ЭП раствора х здесь обозначена буквой k

0 5 10 4 0.001

Во-первых, мы не видим в области малых концентраций KCl мешающего влияния углекислого газа, присутствующего в использованной нами в качестве растворителя однократно дистиллированной воде. В противном случае мы не наблюдали бы изменения удельной ЭП раствора при уменьшении концентрации электролита или заметили бы выход на горизонтальную асимптоту - выполаживание кривой k - o при малых концентрациях (по-видимому, это начинает обнаруживаться при o < 110-5 м/л).

Во-вторых, расчет эквивалентной ЭП и построение соответствующих графиков в координатах закона Кольрауша показывает, что этот закон не выполняется. Впрочем, он плохо вы-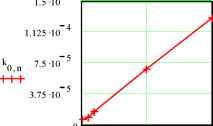

полняется для того же раствора KCl и в случае, если воспользоваться данными справочника [2], рис.2. Экстраполяция прямых Хс-у[с , построенных по этим данным, к нулевой концентрации на графиках Б и В дает близкие значения 129.9 и 128.1 ом-1.г-экв-1.см2. Что же касается графика А, то интересно, что практически к тому же результату А, = 127.2 ом-1.г-экв-1.см2 приводит экстраполяция данных по эквивалентной ЭП к нулевой концентрации, если это делать не в

координатах уравнения Кольрауша, т.е. Ас - л/с , а в координатах А1о - 1/o15, рис.3.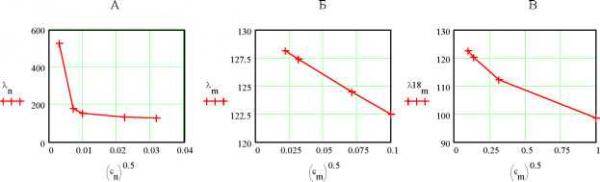

Рис.2. Характер изменения эквивалентной электропроводности водных растворов KCl; t = 18oC. А - по данным авторов, Б и В - согласно справочным данным [2] для интервалов концентраций соответственно 0.0005 - 0.01 и 0.01 - 1 м/л

0, n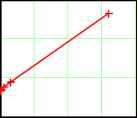

Рис.3. Зависимость эквивалентной ЭП от корня степени -3/2 из концентрации раствора KCl в воде

1 10

Взаимное совпадение значений Ас и А10 свидетельствует по нашему мнению о корректности выполненных нами бесконтактных измерений [1], что t107 позволяет перейти к дальнейшему анализу полученных данных.

Рассмотрим эволюцию изменений удельной ЭП в зависимости от температуры (табл.3, [1]), что графически представлено на рис.4. Из этого рисунка следует, что в области пониженных температур, в интервале примерно 18 - 24оС, ход всех пяти кривых происходит практически параллельно одна другой, а в интервале 24 - 30оС эта параллельность нарушается и тем сильнее, чем ниже концентрация раствора.

2 10 3 10

3 4 5 2

Рис. 4. Изменение ЭП водных растворов KCl с температурой и концентрацией по данным

авторов: 1 - 110-5, 2 - 510-5,

3 - 110-4, 4 - 510-4, 5 - 110-3

Для удобства рассмотрения и сопоставления данных кривых друг с другом их ординаты изменены введением коэффициентов 0.55, 1, 4, 6 и 8 соответственно для кривых 1 - 5

9 -10

8 -10

7 -10

6 -10

5 -10

4 10

Таким образом, при температура 24оС по-видимому происходит перестройка структуры раствора. В этой связи представляется целесообразным проанализировать имеющиеся в справочном материале данные по температурным зависимостям электропроводности растворов KCl и плотности воды. Так на рисунке 5 приведены кривые удельной ЭП, построенные по данным [2]. Они аналогичны нашим кривым, рис.4, хотя в явном виде на них (рис.5) и не видно сингулярностей, которые можно было бы истолковать как результат структурных перестроек.

0.15 I-1

n1 -5

2.610

0.05

102030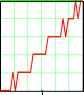

0 5.5 11 16.522 27.5 33 n1

5.6 10 5.4 10 5.2 -10 dk2n2 5 10 -4.8 -10

4.6 10 4 . 4 1 0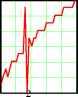

2.12 10

0 7 14 21 28 35 n2

Рис.5. Зависимость удельной ЭП водных растворов KCl при t = 18оС по данным [2]. Концентрации растворов снизу вверх: 0.01, 0.02, 0.1, 1.0 м/л

3 10

2.78 -10

2.56 10

n32.34 -10 4

1 . 9 1 0

0.00235

0.00208

--3-

0 7 14 21 28 35 n3

0.00181

0 . 0 0 1 54

Рис.6. Зависимость от температуры производной (приращений) удельной ЭП водных растворов KCl по температуре; концентрация растворов: 1 - 0.01, 2 - 0.02, 3 - 0.1, 4 - 1.0 м/л (согласно данным, рис.5)

Однако если взять производные удельной ЭП по температуре или, что все равно, соответствующие приращения % между соседними точками, то обнаруживается обилие сингулярно-стей, количество которых уменьшается с ростом концентрации электролита, рис.6. По-видимому, это связано с тем, что структурные перестройки происходят собственно в растворителе- воде. С ростом концентрации KCl структура воды все более разрушается и число ее структурных модификаций соответственно уменьшается. В чистом виде это обнаруживается на аналогичных зависимостях плотности воды от температуры. При этом снова интегральные кривые, как в области средних (0-55оС), рис.7А, так и, тем более, в области повышенных температур (55-100оС), рис.7Б, не обнаруживают структурных перестроек. В то же время дифференциальные кривые для области температур 0-55оС, рис.7В, показывают почти непрерывные структурные переходы с резким структурным скачком при 36-38оС (нормальная температура тела человека 37оС !), а в области температур 55-100оС , рис.7Г, эти перестройки не наблюдаются.

Структурные перестройки отражаются и на диэлектрической проницаемости, рис.8. Здесь мы видим, что при малых концентрациях хлорида калия (с = 1.10-5 м/л, рис.8 А,1) в интервале температур 24-27оС диэлектрическая проницаемость не меняется. Можно представить, что интервал 24-27 оС является одним из островков устойчивости структуры раствора. С ростом

концентрации электролита структурные перестройки под влиянием температуры становится все менее заметными, и при концентрации 1.10-3 м/л мы наблюдаем практически линейный спад ДП с ростом температуры.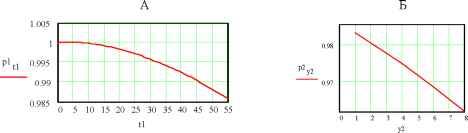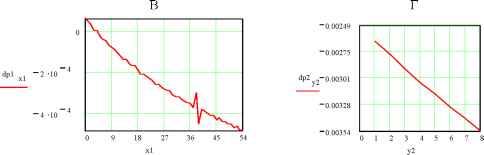

Рис.7. Зависимость плотности воды от температуры А - 0-55оС и Б -55-100оС, а также ее производной по температуре (В и Г); в целях удобства обработки этих данных интервал 55-100оС на диаграммах Б, В и Г разбит на восемь равных отрезков

Общую картину зависимости ДП от температуры и концентрации KCl можно видеть на рис.8 Б. Обращает на себя внимание тот факт, что при концентрациях электролита, не превышающих 1.10-4 м/л, его влияние на ДП раствора очень мало, и все три кривые (1-3) сливаются. Однако при дальнейшем росте концентрации KCl, с переходом в следующий порядок (с = 5.10-4 м/л), диэлектрическая проницаемость начинает заметно уменьшаться. При концентрации

А Б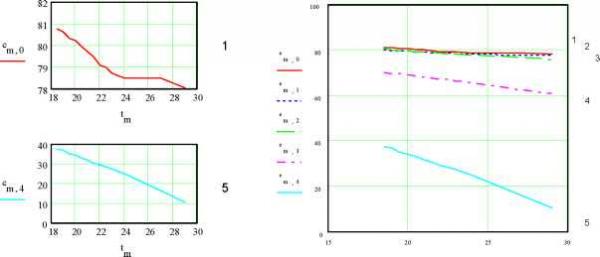

Рис.8. Изменение ДП (на графиках ДП обозначена e ) водных растворов KCl с температурой и концентрацией: 1 - 110-5, 2 - 510-5, 3 - 110-4, 4 - 510-4, 5 - 1.10-3 м/л. А) Кривые для растворов с концентрациями 1 и 5. Б) Семейство кривых для растворов всех исследованных концентраций 1 5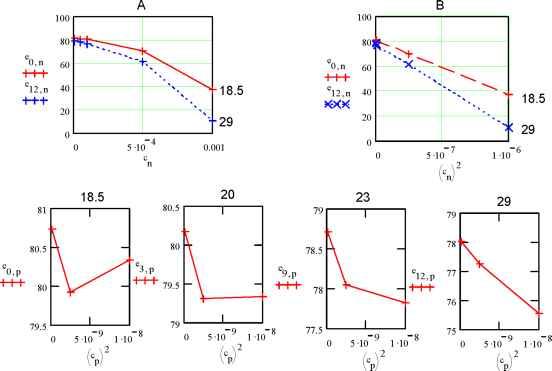

Рис9. Зависимость диэлектрической проницаемости водных растворов KCl от

же 1.10 , что является примерной границей перехода от классической теории растворов электролитов Дебая, Гюккеля, Онзагера [3], наблюдается линейный спад ДП с ростом температуры (рис.8А,Б.5).

Конечно, возникает законный вопрос, не вызвано ли столь значительное снижение (табл.3 [1]; рис. 8, кривая 5) величины ДП с ростом температуры и концентрации раствора методическими причинами и примененными нами в работе [1] способами калибровки ячейки? Однозначно решить этот вопрос можно было бы сопоставлением с литературным материалом. Однако достоверные справочные данные такого рода в литературе отсутствуют. Что же касается весьма авторитетного справочника [4], то имеющиеся в нем сведения (с.269) о диэлектрической проницаемости водных растворов KCl для рассматриваемой области концентраций вызывают сомнения. Оригинальные работы, на которые ссылается автор [4], относятся к периоду 1927 - 1939 г.г., когда измерения такого рода производились без учета соотношения токов проводимости и токов смещения. Но именно этот вопрос является кардинальным и, как выше отмечено, не имеющим удовлетворительного решения и до настоящего времени. С учетом этих замечаний и принимая во внимание удовлетворительное согласие наших и справочных значений удельной ЭП исследованных растворов, мы будем акцентировать внимание при дальнейшем анализе не столько на конкретных значениях искомых величин % и г, сколько на тенденциях и закономерностях их изменений. Так температурная зависимостьДП при различных концентрациях электролита оказывается не столь простой, как это представлено на рис.8

Во-первых, концентрационные изотермы представляют собой не прямолинейные, а криволинейные (выпуклые) функции. Интересно, что последние спрямляются, если по оси абсцисс откладывать концентрацию не в первой (рис.9А), а во второй степени (рис.9В), причем эти прямые характеризуется достаточно высокими значениями коэффициентов корреляции: Koorr = 0.99987 (18.5оС), 0.99976 (19оС), 0.99984 (19.5оС), 0.99986 (20оС), 0.99990 (20.5оС), 0.99991 (21оС), 0.99988 (21.5оС), 0.99991 (22оС), 0.99980 (22.5оС), 0.99995 (23оС), 0.99993 (24оС), 0.99978 (27оС) , 0.99974 (29оС). Во-вторых, указанная прямолинейность исчезает, если рассматривать лишь область малых концентраций, рис.9, где обнаруживается уже не выпуклость, а минимум, рис.12 (18.5оС). При возрастании температуры этот минимум постепенно исчезает. Данный процесс количественно также может быть охарактеризован коэф-

концентрации в первой степени (A), во второй степени (B) и от температуры; последняя указана сбоку кривых A,B и сверху четырех графиков нижнего ряда

фициентом корреляции к прямой линии, так сказать, разбросом экспериментальных точек относительно ниспападающих прямых, как на рис.8. Значения Koorr для температур 18.5,

21, 20, 22, 23, 24, 27, 29оС таковы: 0.22794, 0.66462, 0.65949, 0.73393, 0.84305, 0.8773,

0.97615, 0.99694. Отсюда следует, что с ростом температуры чувствительность ДП к изменениям структуры быстро снижается. В то же время ЭП раствора, как мы видели, замечает структурные переходы по крайней мере до температур порядка 50оС.

Плазменные колебания в растворах электролитов

Рассмотренные выше корреляции электрических свойств растворов электролитов с их структурой дает основание для установления между ними более глубоких функциональных связей. В этой связи обратим внимание на нетрадиционный подход к пониманию механизма ЭП, отмеченный во введении, и воспользуемся представлениями физики полупроводников [5,6], согласно которым удельная ЭП:

e n-г

Х =-*- , (1)

где e - заряд электрона, n - число носителей тока (электронов или дырок) в 1 см3, г* и m* - их эффективные время релаксации и масса.

В работах [7-9] показано, что концентрация носителей тока в растворах электролитов на два-четыре порядка меньше, чем концентрация ионов электролита. С учетом этого замечания можно величину n в (1) заменить произведением koNA, т.е. записать

n = koNA, (2)

где k = 10-4, с - концентрация электролита (м/л) и NA - число Авогадро. Сочетая (1) и (2) и решая полученое уравнение относительно времени релаксации, находим

г = m ЧтТГ > С3)

e kN A

где tga = x/o - тангенс угла наклона зависимости удельной ЭП раствора от его концентрации. Согласно данным табл.3 значения tga для температур 18.5 и 29оС соответственно равны 126.5 и 156.7 с-1 см3. Подставим в уравнение (3) среднее этих значений (141.6 с-1 см3) и примем k = 10-4 (ур.2), т. е. нижнему пределу отношения концентрации носителей тока к концентрации ионов электролита. Будем также считать, что эффективная масса носителей тока в водных растворах KCl m*=0.01m [8,10] (m - масса электрона). В результате получаем т* = 0.93010-28 с. Не останавливаясь на физической стороне очень малого значения т*, рассмотрим этот вопрос с другой стороны.

В числе основных составляющих величины т физика полупроводников рассматривает вклад процесса рассеяния носителей тока на тепловых колебаниях решетки [6, с.275]:

9-тс M -со 2 -Ы4 L

4-2/2 Q-G2 -me15 -Kb -T

т

где M - масса атома, ю - скорость продольной звуковой волны, h1 = h/2n - постоянная Планка, L - нормирующий множитель ([L] = [длина, 1 см], вводимый для удовлетворения требованиям размерности: [т] = [с-1]. Q - объем элементарной ячейки, G - константа взаимодействия элек-

тронов с фононами, me - масса электрона, Kb - константа Больцмана, T - абсолютная температура, ее - эффективная диэлектрическая проницаемость. Последняя включает в себя показатель преломления p и es - статическую ДП раствора:

-1 -2 -1 ее = p + es .

Для расчетов согласно (4) сделаем следующие допущения. Будем считать, что атомами, образующими решетку, в которой распространяется звуковая волна, являются протоны, т.е. M

= 1.67 10 г. Предположим далее, что величина ю численно равна частоте, отвечающей звуковой волне, и эта частота соответствует температуре 25оС, т.е.

T : = ( 273 -h 25 ) K

- Kb./h

ю = 2nv.

Заметим также, что величина т в ур. (4) будет отвечать размерности времени, если константа

5/4 2 -5/2

электрон-фононных взаимодействий [G] = [г см с ] . И, наконец, будем считать, что объем элементарной ячейки Q = 4/3.пр3 определяется диаметром молекулы воды, т.е. р ~ 3.10-8 см. При учете указанных допущений оказывается, что согласно (4) т = 0.91610-28 с.

Столь поразительное совпадение результатов расчета согласно уравнениям (3)и (4), т.е. т* = т (!). дает нам основание, во-первых, считать, что вероятность электрон-фононных взаимодействий в растворах весьма велика (G = 1, а размерность этой величины

5/4 2 -5/2

действительно [г см с ]). При этом заметим, что нахождение константы электрон-фононных взаимодействий G является центральной и наиболее сложной задачей при изучении рассеяния носителей тока в твердых полупроводниках на тепловых колебаниях решетки [6, с.275]. Во-вторых, исходя из тех же соображений, можно выполнить аналогичные оценки и в отношении диэлектрической проницаемости. Так, исходя из равенства т* = т, подставляя в это равенство выражения (3), (4) и решая полученное уравнение относительно ДП, получаем:

s = n

где

9п

Mm2 h14

y2 .3/2i

m* 4V2 OG2m3,2кБT Заменяя n согласно (2), находим:

fx >

(kcNа )2

f X kN А Л Х

В этом выражении tg(P) = е/o2 характеризует тангенс угла наклона прямых, рис.9В, среднее значение которого для интервала температур 18.5-29оС равно 5.551013см6. Учитывая, что X определяется выражением (8) и решая (9) относительно ю получаем:

=>

a= tgтхаа-m к.т^ , (10)

v kNAe29nMh/2п J

где k = 10-4.

При выполнении расчетов в этом и во всех других ранее указанных уравнениях необходимо учитывать следующие размерности: [tg(a}] = [с-1см3], [tg(P)] = [см6], [%] = [с-1], [m*,m,M] =[г], [G] = [г5/4см2с-5/2], [KБ] = [гсм2с-2К-1], [e] = [см1.5г05с-1], [h] = [гсм2с-1], [T] = [K], [L] = [см-1].

Кроме того, в знаменателе (10) должна стоять величина L. Однако она опущена, поскольку ее значение принято равным единице.

При k = 10-4, tg(P) = 5.551013, m* = 0.01m, p = 3.10-8 (примерный радиус молекулы воды), T = 297 (t = 24оС, как среднее для температур 185-29°С) и M = 1.6710-24 (масса протона) получаем для растворов KCl и концентраций 0.00001, 0.00005, 0.0001, 0.0005, 0.001 м/л следующие значения:

ю = 1.205 1 09, 7.651 109, 1.998.1010, 2.104 1 011, 5.881 1011 рад/с. (11)

Чтобы понять физический смысл этих значений обратимся к теории гармонических колебаний, точнее к вопросу электрических колебаний в плазме [11, с.502: 12,с.133-146]. Эти колебания вызываются силами электрического поля. Эти колебания возникают в среде при каком-либо случайном отклонении пространственного распределения электронов от равновесного. Круговая частота этих колебаний, называемая плазменной или ленгмюровской, описывается уравнением [12, с.134; 13, с.262]:

V ms

(12)

Полагая, как и раньше, что концентрация носителей тока на четыре порядка меньше концентрации электролита (k = 1.10-4), концентрация раствора KCl o = 0.00001, 0.00005,

0.0001, 0.0005, 0.001 м/л n = 10-4.oN

/ ? ---

78.5 - 24.4 ([1],табл.3, 24оС), находим

9.172109, 2.051 1010, 2.91010, 6.471 1010, 8.935 1010 рад/с.

(13)

Несмотря на различный концентрационный ход величин ю и cgp, рис.10а между ними обнаруживается замечательная связь, рис.9б, характеризующаяся высоким значением коэффициента корреляции 0.99998. Интересно также, что в предположении, что вогнутая кривая ю - концентрация раствора (на рисунке 10а, Fn - on) при дальнейшем росте концентрации раствора окажется S-образной кривой, то началу выполаживания в верхней части этой кривой будет отвечать концентрация 3.6.10-3 м/л, которой соответствует частота ю = 1.6651016 с-1 (при расчетах в MathCad эта частота обозначена Fpl):

6 -10 5 -10 4 -10 3 -10 2 -10 1-10

б

0.01

0.02 \0.5

0.03

0.04

-4 -4 -4 -4

2 -10 4 -10 6 -10 8 -10

0.001

а

Рис.10. Зависимости частоты продольных звуковых колебаний Fn (вогнутая кривая, - в тексте ю) и частоты плазменных колебаний юп (прямая линия, - в тексте cop) в водных растворах KCl при 24оС от корня квадратного из концентрации (а) и взаимная корреляция этих частот (б)

onn:=(on)L5 Fpl:=interp(lspline(cn,F),on,F,0.023515) Fpl = 1.665-1016 seo 1 0.023515 = 0.0036 . (14)

А это есть частота плазменных колебаний в металлах [12, с.135]. Такие колебания могу существовать, если диэлектрическая проницаемость обращается в нуль [12, с. 142]. Возможно, что отмеченное нами выше значительное снижение ДП в правом нижнем углу таблицы 3 [1] происходит вследствие этой особенности плазменных колебаний в растворах электролитов.

Другой особенностью плазменных колебаний является то обстоятельство, что при этом вся электронная структура кристалла осциллирует в фазе. Поскольку в нашем случае мы имеем дело не с кристаллом, а с жидкостью, имеющей пространственную сетку водородных связей, то естественно предположить, что и в водных растворах электролитов электроны, образующие наряду с протонами эту сетку, также могут совершать синфазные плазменные колебания. Конечно, порог возникновения таких колебаний должен зависеть от температуры, концентрации растворенного электролита, его природы и температуры. Вполне возможно также, что именно этим и обусловлено существование так называемой предельной высокочастотной (ПВЧ) электропроводности (ЭП) жидкостей и растворов с водородными связями [14-16; 17, с.168]. Эффект ПВЧ ЭП означает, что индивидуальный растворитель уже изначально имеет электропроводность, превышающую таковую в растворах электролитов и в том числе в растворах кислот и щелочей, и что ПВЧ обусловлена именно плазменными колебаниями, существующими в жидкостях, ассоциированных благодаря водородным связям.

Рассмотрена зависимость удельной ЭП растворов KCl в интервале концентраций !0-5 -10-3 м/л и температурах 18-29оС. Показана связь электрических свойств растворов электролитов (электропроводности и диэлектрической проницаемости) с их структурой. На основе представлений физики твердого тела обсуждается природа носителей тока в растворах электролитов. Сделан вывод о возможности плазменных колебаний в системе их водородных связей. Обосновано предположение о том, что именно плазменными колебаниями обусловлен эффект предельной высокочастотной электропроводности в растворителях с водородными связями и в растворах электролитов.

Литература

1.Фенин А. А., Фенин С. А., Ермаков В.И. Электропроводность, характеристики носителей тока, диэлектрическая проницаемость и структура растворов электролитов. I. Измерение электропроводности и диэлектрической проницаемости методом выделения составляющих импеданса.

2. Справочник химика. Т.3. с.664. Химия. М.-Л. - 1964. 1005 с.

3. Измайлов Н.А. Электрохимия растворов.. Изд-во Харьковского Ордена Тр. кр.знамени гос. Ун-та им. А.М. Горького. Харьков.-1959. 958 с.

4.Ахадов Я.Ю. Диэлектрические свойства чистых жидкостей. с. 52,59. Изд-во стандартов. М.- 1972. 412 с.

5. Киреев П.С. Физика полупроводников.. Высшая школа. М.-1975. 584 с.

6. Стильбанс Л. С. Физика полупроводников.. Советское радио. М.-1967. 451 с.

7. Lafarque-Kantzer D. Effekt magnetoeleotrique des solutions daoides mineraux. Eleotroohim. Aota. 1965. V.10. P. 585-603.

8. Чембай В.М. Влияние температуры, концентрации и состава растворов электролитов на их электрические свойства. ДисCKанД'XиMH МХТИ им. Д.И. Менделеева. М.-1988.163 с.

9. Ермаков В.И., Чембай В.М. Электропроводность многокомпонентных растворов электролитов. РХТУ им. Д.И. Менделеева. М.-1995. 47 с.

10. Фенин С. А. Электропроводность и характеристики носителей тока в бинарных водных растворах NaCl+KCl, KCl+MgCl2, MgCl2+BaCl2 и водно-органических растворах NaCl. Дисс. канд. хим. н. РХТУ им. Д.И. Менделеева. М.-2003.

11. Капцов Н.А. Электрические явления в газах и вакууме. Гос. изд-во техн.-теорет. лит. М.-Л.-1950. 836 с.

12. Слэтер Дж. Диэлектрики и полупроводники. Мир. М.-1969. 647 с.

13. Яворский Б.М., Детлаф А.А. Справочник по физике. Наука. М.-1985. 512 с.

14. Щербаков В.В., Ермаков В.И. Комплексная и предельная высокочастотная электропроводность коцентрированных растворов электролитов. Ж. Физ. Химии. 1977. Т.51, №7, 17841787 с.

15. Щербаков В.В., Ермаков В.И. Высокочастотная проводимость растворов электроли-тови диэлектриков. Электрохимия. 1977. Т.13. №7, 1091-1092 с.

16. Щербаков В.В. Закономерности в электропроводности и диэлектрических характеристиках двухкомпонентных и трехкомпонентных растворов неорганических электролитов. Дисс. докт. хим. н. МХТИ им. Д.И. Менделеева. М.-1992. 440 с.

17. Ермаков В. И. Диэлектрическая радиоспектроскопия. В кн. Экспериментальные методы химии растворов. Наука. М.-1995. 380 с.