ЗАО

Граничная конвекция

Поток тепла через границы

Боковая конвекция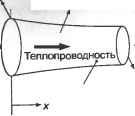

Поток тепла через границы

Внутренний источник тепла

Граничная конвекция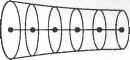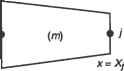

Рис. Л.1. Пример одномерной задачи распространения тепла

Решение

Как можно узнать из большинства учебников по распространению тепла, основное уравнение для температуры Т в стержне имеет вид

d (, лdT

kA- dx

У

hP(T-Ta) + QA=0.

(Л.6)

Применяя метод взвешенных остатков, получаем

MkA* dx\ dx

У

hP(T -Ta) + QA

dVim) =0 (i = 1,2,..., n), (Л.7)

где n - это общее число узлов, а знак суммирования т обозначает суммирование по всем элементам.

Для конкретного случая метода Галеркина уравнение (Л.7) принимает вид

dVim) =0,

(Л.8)

ix{Mix~)~hP{:ir~Ta)+QA

где матрица-столбец N - это матрица функций формы. Таким образом, (Л.8) представляет собой систему из п уравнений, каждое из которых соответствует одному из элементов N. Матрица функций формы была определена, когда было сделано предположение о распределении температуры в стержне:

Т =NTT, (Л.9)

где Т - это матрица-столбец температур в узловых точках.

Временно проигнорируем символ суммы в уравнении (Л.8), поскольку мы легко сможем произвести суммирование, когда выведем общее выражение для элемента т. Типичный элемент т соединяет узлы i uj с координатами X; и X, соответственно (рис. Л.1, в). Исходя из этого, (Л.8) можно переписать так:

[* AT-{kAP\-hP{T-Ta)+QA dx=0. (Л.10)

lxi \ dx\ dx)

Формулировка системных уравнении конечноэлементного анализа

Обратите внимание, что элемент объема dv заменяется на A dx, где А - это площадь поперечного сечения в точке X.

Интегрируя первое слагаемое по частям и опустив постоянную площадь, получим

ША dx

XJ ~ С ff л -С mpTdx+С ШРТ^+С NQAdx=°- <лл

Когда будет выполнено суммирование по всем элементам, первое слагаемое каждого элемента в уравнении (Л.11), кроме первого и последнего, уничтожится, поскольку в следующий элемент входит такое же слагаемое с обратным знаком. Поэтому данное слагаемое достаточно вычислить только для элементов с номерами 1 и М, если считать, что элементы нумеруются последовательно, а М - это общее число элементов.

Чтобы вычислить это слагаемое для первого и последнего элемента, рассмотрим один из концов тела (рис. Л.2). Внешний поток тепла обозначен как qs, поток тепла, обусловленный теплопроводностью, - qx, а поток тепла за счет конвекции - qat.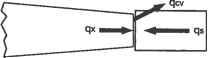

Рис. Л.2. Теплообмен на границе в одномерной задаче распространения тепла Баланс энергии на этом конце тела дает

или

Qx=Qa,-Qs- (Л. 12)

Мы знаем, что поток тепла, обусловленный теплопроводностью, согласно закону теплопроводности Фурье может быть выражен в виде

,dT qx =-k-. dx

(Л. 13)

Используя формулы (Л. 12) и (Л. 13), можно вывести следующее выражение для

NkA- в уравнении (Л.11)1 при х = Х-.

ША-dx

= N(-qxA)\x=x. =NAj(-qcv+qs)\x=Xj = = -К/гуЛ.(7--7-ч/.)+Ш^, =-NA7.i47T+NA7.r +NAW,J

(Л.14)

1 Поток тепла за счет конвекции qa, равен hfj- Tuj), где Taj - это окружающая температура при х = Xj. Более того, qs в точке х - Xj заменяется на qj в узле/ Вспомните, что точка х = Xj обозначает один из концов стержня.

i luniiuncnne j i. члзрмулириькс! системных уравнении конечноэлементного анализа

Аналогичное выражение получается для N&A - при х = X/.

(Л.15)

д=А', i

Обратите внимание, что равенство (Л.14) выполняется только для последнего элемента, а равенство (Л.15) - только для первого элемента, как было сказано ранее.

Подставляя уравнения (Л.9), (Л.14) и (Л.15) в уравнение (Л.11), получим: (-NhjAj7VTT + NhjAjTaj +ТЧЛ, )\X=X) +

+ (-N/z,AiVTf + Kh,A,Tai )U,- (Л.16)

rA kATdx -\x> mmTTdx + fA шртиах + fAj Ncvkfr = o.

Ja. dx dx Ja- Ja. j*.

Вынося Тза пределы интегрирования в уравнении (Л.16), получаем следующее уравнение для элемента т:

Klm>f = f(M), (Л.17)

где матрица жесткости элемента К<т) состоит из трех матриц жесткости, или матриц проводимостей:

к1 0 =к[т) +к,(;:0 + k( J, (л.18)

а узловой вектор силы элемента f(и) состоит из четырех векторов силы:

f < ) = f <;> + f£ + + fv<;> (Л.19)

Матрицы в уравнениях (Л.18) и (Л.19) определяются следующим образом:

К[т) = Г* -kA-dx\

Jx dx dx Ja-,

Km) = N/zpN T dx; K<:> =NA,.AfNTjri+NA>NTxJ;

f,<;> =fjmvradx; С =N9l.AU-,+N?HyLAV

Имея все матрицы жесткости и узловые векторы силы элементов, мы суммируем их, чтобы получить системную матрицу жесткости и узловой вектор силы в форме, данной в главе 8. Слагаемые с символом В в нижних индексах имеют ненулевые значения только для первого и последнего элементов суммы.

1 Источник: Computer Graphics World. Vol. 20, No. 5, May 1997, PennWell Publishing Company.

Сравнение CAD-систем на платформе Windows1

Таблица М.1. Сравнение CAD-систем на платформе Windows

Характеристика

Минимальный объем ОЗУ, Мбайт

Требуемый объем дискового пространства, Мбайт

ТребуемыГ1 объем пространства для файла подкачки, Мбайт

Ядро геометрического моделирования

Технология моделирования (параметрическое, вариационное, объектно-ориептнрованное)

Использование истории

Моделирование поверхностей

Моделирование агрегатов

CADKEY 97

$1195

ACIS 2.1

Гибридное моделирование произвольных форм

Нет

Да, с использованием программ сторонних производителей (FastSURF)

Euclid Quantum 1.0

$9995 96

2000

CAS. CADE

Явное, вариационное, параметрическое, объектно-ориентированное

Частичное -

в надлежащих случаях

Helix Design System V4

$5695

DesignBase

Вариационное, параметрическое, объектно-ориентированное

I DEAS Artisan Series 1.0

$4995

Собственное

Явное, гибридное, вариационное, параметрическое, объектно-ориентированное

Да, с использованием программ сторонних производи-телей

Характеристика

Минимальный объем ОЗУ, Мбайт

Требуемый объем дискового пространства, Мбайт

Требуемый объем пространства для файла подкачки, Мбайт

Ядро геометрического моделирования

Технология моделирования (параметрическое, вариационное, объектпо-ориентированное)

Mechanical Desktop VI.2

$6250 ($2750 в случае перехода с AutoCAD)

MicroStation Modeler V5.5

ACIS 1.6

Явное, булевское, вариационное, параметрическое, объектно-ориентированное

Использование истории

Моделирование поверхностен

Моделирование агрегатов

Параметрическое моделирование

Да, система параметрического моделирования использующая размерные и геометрические ограничения

$5325 ($4975, если также приобретается обслуживание Bentley SELECT)

Pro/Engineer 18.0 Advanced Designer Package

$26 000, включая Pro/E и 13 модулей

SolidDcsigner V4.5

ACIS 2,1

Явное, булевское, вариационное, параметрическое, объектпо-орпептнроваппое

Собственное (Рго/Е)

Параметрическое, объектно-ориентированное

$6500

Расширенное AC1S

Объектпо-орпептировапное

Да, для создания элементов, связей и твердых тел

Да, система объектно-ориентированного моделирования на параметрической основе, таблицы семейств, агрегаты и связи, а также среда для построения эскизов с автоматическим масштабированием

Да (дополнительный модуль)

Дополнительно (позволяет применять динамические связи)

Литература

1. Amirouche, М. L. A Computer-Aided Design and Manufacturing, Co. Prentice Hall, Englewood Cliffs. NJ, 1993.

2. Armstrong, C. G. Modeling Requirements for Finite-element Analysis*, Com-puter-Aided Design, Vol. 26, No. 7, pp. 573-578, 1994.

3. Armstrong, C. G., Robinson, D. J., Mckeage, R. M., Li, T. S., Bridget!, S. J., Do-naghy, R. J., and McGleenan, C. A. Medials for Meshing and More , 4th Annual International Meshing Roundtable, (sponsored by Sandia National Laboratories), October 16-17, 1995.

4. Anderson, R. O., Detecting and Eliminating Collisions in NC Machining*, Com-puter-Aided Design, Vol. 10, No. 4, pp. 231-237, 1978.

5. Ashley, S. Manufacturing Firms Face the Future*, Mechanical Engineering, pp. 70-74, June 1997.

6. Avriel, M. Nonlinear Programming-Analysis and Methods, Prentice-Hall, Englewood Cliffs, NJ, 1976.

7. Barfield, W. and Furness, Т. A. III. Virtual Environments and Advanced Inter face Design, Oxford University Press, New York, 1995.

8. Barnhill, R. E., Birkhoff, G, and Gordon, W. J. Smooth Interpolation in Trian gles ,J. Approx. Theory, Vol. 8, pp. 114-128, 1973.

9. Bartels, R. H., Beatty, J. C, and Barsky, B. A. An Introduction to Splines for Use in Computer Graphics and Geometric Modeling, Morgan Kaufmann Publishers, Los Altos, CA, 19,87.

10. Bathe, K.-J. Finite Element Procedures in Engineering Analysis, Prentice Hall, Englewood Cliffs, NJ, 1982.

11. Baumgart, B. Winged-edge Polyhedron Representation*, Stanford Artificial Intelligence Report No. CS-320, 1972.

12. Baumgart, В. A Polyhedron Representation for Computer Vision*, Proceedings of the National Computer Conference, 1975.

13. Beasley, D., Bull, D. R., and Martin, R. R. An Overview of Genetic Algorithm: Part I, Fundamentals*, University Computing, Vol. 19, No. 2, pp. 58-69, Inter-University Committee on Computing, 1993.

14. Beckert, B. A. Venturing into Virtual Product Development*, Computer-Aided Engineering, pp. 45-50, May 1996.

15. Bedworth, D. D., Henderson, M. R., and Wolfe, P. M. Computer Integrated Design and Manufacturing, McGraw-Hill, New York, 1991.

Irian-

>r I Tsf>

16. Beier, К. Virtual Reality in Automotive Design and Manufacturings SAE Technical Paper 94C030, 1994.

17. Bendsoe, M. P. and Kikuchi, N. Generating Optimal Topologies in Structural Design Using a Homogenization Method , Computer Methods in Applied Mechanics and Engineering, Vol. 71, pp. 197-224, 1988.

18. Bendsoe, M. P., Diaz, A., and Kikuchi, N. Topology and Generalized Layout Optimization of Elastic Structures*, In Bendsoe and Scares (eds.), Topology Design of Structures, Kluwer Academic Publishers, Dordrecht, Holland, 1992.

19. Bezier, P. The Mathematical Basis of the UNISURF CAD System, Butterworths, London, 1986.

20. Boehm, W., Farm, G, and Kahmann, I. A Survey of Curve and Surface Methods in CAGD , Computer-Aided Geometric Design, Vol. 1, pp. 1-60, 1984.

21. Boehm, W. and Prantzsch, H. Geometric Concepts for Geometric Design , A. K. Peters, Wellesley, MA, 1994.

22. Botkin, M. E., Yang, R. J., and Bennett, J. A. Shape Optimization of Three-dimensional Stamped and Solid Automotive Components*, in The Optimum Shape, Plenum Press, New York, 1986.

23. Braid, I., Hillyard, R., and Stroud, I. Stepwise Construction of Polyhedra in Geometric Modeling*, CAD Group Document No. 100, Cambridge University Computer Laboratory, 1978.

24. Breltinger, F. Rapid Tooling for Simultaneous Product and Process Development: Part II , RapidNEWS, Vol. 5. No. 6, pp. 52-57,1997.

25. Briabant V. and Fluery, C. Shape Optimal Design Using B-splines , Computer Methods in Applied Mechanics and Engineering, Vol. 44, No. 3, pp. 247-267, 1984.

26. Budynas, R G. Advanced Strength and Applied Stress Analysis, McGraw-Hill, New York, 1977.

27. Bykat, A. Automatic Generation of Triangular Grid: I-Subdivision of a General Polygon into Convex Subregions; II-Triangulation of Convex Polygons , Int. J. Numer. Meth. Eng., Vol. 10, pp. 1329-1342, 1976.

28. Carrington, J. Modeling Entire Products*, Computer-Aided Engineering, pp. 30-34, August 1997.

29. Cavendish, J. Automatic Triangulation of Arbitrary Planar Domains for the Finite Element Method*, Int. J. Numer. Meth. Eng, Vol. 8, pp. 679-696, 1974.

30. Cavendish, J. C, Field, D. A, and Frey, W. H. An Approach to Automatic Three-dimensional Finite Element Mesh Generation*, Int. J. Numer. Meth. Eng., Vol. 21, pp. 329-347, 1985.

31. Cerny, V. Thermodynamical Approach to the Traveling Salesman Problem: An Efficient Simulation Algorithm*, J. of Optimization Theory and Applications, Vol. 45. No. 1.1985.

32. Chang, Т. C, Wysk, R. A., and Wang, H. P. Computer Aided Manufacturing, 2nd ed., Prentice-Hall, Englewood Cliffs, NJ, 1998.

33. Chapman, C. D. Structural Topological Optimization via the Genetic Algorithm*, MS thesis. Dept. of Mech. Eng., MIT, 1994.

34. Chappel, I. T. The Use of Vectors to Simulate Material Removed by Numerically Controlled Milling*, Computer-Aided Design, Vol. 15, No. 3, pp. 156-158, 1983.

35. Chiyokura, H. Solid Modeling with DESIGNBASE: Theory and Implementation, Addison-Wesley, Reading, MA, 1988.

36. Clough, R. W. The Finite Element in Plane Stress Analysis*, Proceedings of 2nd A.S.C.E. Conference on Electronic Computation, September, 1960.

37. Cohen, E., Lyche, Т., and Riesenfeld, R. Discrete B-spIines and Subdivision Techniques in Computer-Aided Geometric Design and Computer Graphics*, Computer Graphics and Image Processing, Vol. 14, pp. 87-101, 1980.

38. Cohen, E., Lyche Т., and Schumaker, L. L. Algorithms for Degree-Raising of Splines*, ACM Transactions on Graphics, Vol. 4, No. 3, pp. 171-181, 1985.

39. Conte S. D. and de Boor, C. Elementary Numerical Analysis, McGraw Hill, New York, 1980.

40. Coons, S. A. Surfaces for Computer-Aided Design of Space Forms*, Technical Report MAC-TR 44, M.I.T., Cambridge, MA, 1967.

41. Cox, M. G. The Numerical Evaluation of B-splines , J. Inst. Maths. Applies., Vol. 15, pp. 95-108, 1972.

42. Crandall, S. H., Karnopp, D. C, Kurtz Jr., E. F., and Pridmore-Brown, D. C. Kurtz Jr., E. F., and Primdore-Brown, D. C. Dynamics of Mechanical and Electromechanical Systems, McGraw-Hill, New York, 1968.

43. de Boor, C. On Calculating with B-spline , J. of Approx. Theory, Vol. 6, pp. 52-60, 1972.

44. Deitz, D. Re-engineering Virtual Prototypes*, Mechanical Engineering, pp. 76-78, September 1997.

45. Drews, P. and Weyrich, M. Virtual Manufacturing*, VR News, Vol. 6, pp. 18-22, 1997.

46. Du, W.-H. and Schmitt, F.J. M. On the Gl Continuity of Piecewise Bezier Surfaces: A Review with New Results*, Computer-Aided Design, Vol. 22, No. 9, pp. 556-573, 1990.

47. Eastman, C. and Weiler, K. Geometric Modeling Using the Euler Operators*, Conference on Computer Graphics in CAD/CAM Systems, May 1979.

48. Farin, G. Curves and Surfaces for Computer-Aided Geometric Design, Academic Press, San Diego, CA, 1990.

49. Faux, I. D. and Pratt, M. I. Computational Geometry for Design and Manufacture, Ellis Horwood, Chichester, Sussex. UK, 1979.

50. Foley, J. D., van Dam, A., Feiner, S. K., and Hughes, J. F. Computer Graphics: Principles and Practice, Addison-Wesley, Reading, MA, 1990.

51. Gain, P. R. New Generation of PDM Emerges*, Computer-Aided Engineering, Vol. 15, No. 11, pp. 52-58, 1996.

Литература

52. Garey, М. R. and Johnson, D. S. Computers and Intractability: A Guide to the Theory of NP-Completeness , Freeman, New York, 1979.

53. Gascoigne, B. PDM: The Essential Technology for Concurrent Engineerings*, 1997

54. Geller, T. L., Lammers, S. E., and Mackulak, G. T. Methodology for Simulation Application to Virtual Manufacturing Environments*, Proceedings of the 1995 Winter Simulation Conference, pp. 909-916, 1995.

55. Goldberg, D. E. Computer-Aided Gas Pipeline Operation Using Genetic Algorithm and Rule Learning*., Ph.D. thesis, Civil Engineering Dept., University of Michigan, 1989a.

56. Goldberg, D. E. Genetic Algorithm in Search, Optimization and Machine Learning, Addison-Wesley, Reading, MA, 1989b.

57. Green, P.J. and Sibson, R. Computing Dirichlet Tessellations in the Plane*, The Computer J. Vol. 21, No. 2, pp. 168-173, 1977.

58. Grefenstette, J. J. A Users Guide to GENESIS Version 5.0, October 1990.

59. Groover, M. P. and Zimmers, E. W. CAD/CAM Computer-Aided Design and Manufacturing, Prentice-Hall, Englewood Cliffs, NJ, 1984.

60. Gursoz, E. L., Choi, Y., and Prinz, F. B. Vertex-based Representation of Non-manifold Boundaries**, in Geometric Modeling for Product Engineering North-Holland, Amsterdam, 1990.

61. Haftka, R. T. and Grandhi, R. V. Structural Shape Optimization-A Surveys*, Computer Methods in Applied Mechanics and Engineering, Vol. 57, pp. 91-106, 1986.

62. Haftka, R. T. and Gurdal, Z. Elements of Structural Optimization, 3rd ed., Klu-wer Academic Publishers, Dordrecht, Holland, 1992.

63. Hartley, P. J. and Judd, C. J. Parametrization and Shape of B-spline Curves for CAD , Computer-Aided Design, Vol. 12, No. 5, pp. 235-238, 1980.

64. Heighway, E. A. A Mesh Generator for Automatically Subdividing Irregular Polygons into Quadrilaterals**, IEEE Transaction on Magnetics, Vol. 6, pp. 2535-2538, 1983.

65. Held, M. On the Computational Geometry of Pocket Machining, Springer-Verlag, Berlin, 1991.

66. Helsel, S. High-Res VR Displays**, Computer Graphics World, pp. 49-54, May 1997.

67. Herrmann, L. R. Laplacian-isoparametric Grid Generation Scheme*, J. of Eng. Mech. Div., Proceedings ofAmer, Soc, Civil Eng., Vol. 102 (EM5), 1976.

68. Hildebrand, F. B. Advanced Calculus for Applications, Prentice-Hall, Englewood Cliffs, NJ, 1976.

69. Hoffmann, С. M., Hopcroft, J. E., and Karasick, M. S. Robust Set Operations on Polyhedral Solids**, IEEE Computer Graphics and Applications, pp. 50-59,1989.

70. Ho-Le, K. Finite Element Mesh Generation Methods: A Review and Classification**, Computer-Aided Design, Vol. 20, No. 1, pp. 27-38, 1988.

Литература

71. Holland, J. H. Adaptation in Natural and Artificial Systems**, University of Michigan, Ann Arbor, 1975.

72. Hoschek, J. and Lasser, D. Fundamentals of Computer Aided Geometric Design, A. K. Peters, Wellesley, MA, 1993.

73. Imam, M. H. ТЪгее-dimensional Shape Optimizations*, Int. J. Num. Meth. Eng., Vol. 18, pp. 661-673, 1982.

74. ISO TC 184 / SC4 / WG5 N9, EXPRESS Language Reference Manual, International Organization for Standardization, 1991.

75. Jacobs, P. F. Rapid Prototyping and Manufacturings*, Society of Manufacturing Engineers, pp. 1-23, 153-220, 1992.

76. Jacobs, P. F. Recent Advances in Rapid Tooling from Stereolithography, 3D Systems, Valencia, С A, 1996a.

77. Jacobs, P. F. Stereolithography and Other RP&M Technologies**, Soc. Manufacturing Engineers, 1996b.

78. Jain, P., Fenyes, P., and Ritcher, R. Optimal Blank Nesting Using Simulated An-nealing , Advances in Design Automation, ASME, DE-Vol. 23, No. 2, pp. 109-116,1991.

79. Jaques, M. W. S., Stickland, P., and Oliver, T. J. Design by Virtual Manufacturing: A Review**, J. Design and Mfg, Vol. 5, pp. 241-250, 1995.

80. Jerad, R. В., Drysdale, R. L, Hauck, K., Schaudt, В., and Magewick, J. Methods for Detecting Errors in Numerically Controlled Machining of Sculptured Surfaces**, IEEE Computer Graphics and Applications, Vol. 9, No. 1, pp. 26-38, 1989.

81. Jones, F. H. and Martin, L. The AutoCAD Database Book, Ventana Press, 3rd ed., 1989.

82. Jung, Y. H. and Lee, K. Tetrahedron-based Octree Encoding for Automatic Mesh Generation**, Computer-Aided Design, Vol. 25, No. 3, 1993.

83. Kalpakjian, S. Manufacturing Processes for Engineering Material, 2nd ed., Addison-Wesley, Reading, MA Р- 541, 1992.

84. Kikuchi, N. Adaptive Grid Design Methods for Finite Element Analysis*, Comput. Meth. Appl Mech. Eng., Vol. 55, pp. 129-160, 1986.

85. Kirkpatrick, S., Gelatt Jr., C. D., and Vecchi, M. P. Optimization by Simulated Annealing**, Science, Vol. 220, No. 4598, pp. 671-680, 1983.

86. Kirsch, U. Optimum Structural Design: Concepts, Methods and Applications, McGraw-Hill, New York, 1981.

87. Kobayashi, K. and Nakazuka, H. STEP Room, Parti: Parametric Definition of Geometric and Topological Representation with Three Schema*, Nikkei Mechanical, pp. 88-99, June 1993 (In Japanese).

88. Kochan, D. Solid Freeform Manufacturing, Elsevier-North Holland, Amsterdam, 1993.

89. Kohn, R. V. and Strang, G. Optimal Design and Relaxation of Variational Problems**, Communic. Pure and Appl. Math., Vol. 39, (Part 1), pp. 113-137; (Part 2), pp. 139-182; (Part 3), pp. 333-350, 1986.