Теорема 6.10.1 Форда и Максимальный поток по

транспортной сети равен мощности минимального т.е.

max cp(z) = minC(A).

Доказательство теоремы - это алгоритм определения максимального потока по сети. Алгоритм состоит из двух частей. Насыщение потока. Поток называется насыщенным, если любой путь изх0 в zсодержит дугу и s U. для которой = с(и). Задача первой части алгоритм состоит в насыщении потока.

1.1. Зададим произвольный начальный поток. Например, нулевой на всех дугах: V4 е ц>(и = 0.

1.2. Поиск пути из в г. Если путь найден, то переход к пункту 1.3. Если путь не найден, то переход к пункту 1.5.

1.3. Увеличиваем поток по найденному пути таким образом, чтобы одна из дут стала насыщенной.

1.4. Условно разрываем насыщенную дугу и переходим к пункту 1.2, на поиск пути из х0 в z.

1.5. Сеть насыщена и разорвана .

2. Перераспределение потока. Итак, поток насыщен, как в примере на рис. 6.24. Пометим рекурсивным образом все возможные вершины сети.

-2 Xl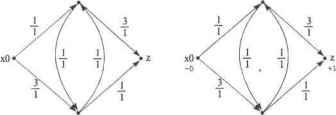

Рис. 6.24. Насыщенная транспортная сеть и пометка вершин

2.1. Вершину пометим -0.

2.2. Пусть - любая из уже помеченных вершин; у - произвольная непомеченная вершина, смежная хг Вершину у помечаем

если данные вершины соединены ненасыщенным ребром xi-*y(+0 и помечаем - /, если соединены непустым ребром После пометки вершин возможны два случая: вершина z оказалась либо помеченной, либо непомеченной.

2.3. Вершина z оказалась помеченной. Значит, существует последовательность помеченных вершин от х„ к z. В этой последовательности каждая последующая вершина помечена номером предыдущей, какнарис. 6.25. Определим на дугах новый поток, увеличивая на единицу поток на дугах, ориентированных по направлению движения к z, и уменьшая поток на единицу на дугах, направленных против этого движения, как на рис. 6.25.

3 13 3 13

-О 1 Щ Г -2 Г +1 2 0 2

хО х2 si z xo х2 xl I

Рис. 6.25. Перераспределение потока на основе пометки вершин

Заметим, что поток можно увеличивать (уменьшать) на прямых (обратных) дугах настолько, пока одна из дуг не станет насыщенной (пустой). Далее вновь переходим к пометке вершин (пункт Выполненное перераспределение потока сохраняет все его свойства и увеличивает на единицу поток в вершину z. Таким образом, пометка вершины z позволяет увеличить поток как минимум на единицу, а значит, алгоритм конечен, т.е. наступит момент, когда вершина z останется непомеченной.

2.4. Вершина z осталась непомеченной. В рассматриваемом примере это показано на рис. 6.26. Пусть А* - множество всех непомеченных вершин. Тогда дуги, входящие в эти вершины, насыщенные, а выходящие - пустые. В примере А* = {xz}. Множество А* определяет разрез, так как Xq еА*, zeA*. Таким образом, мы нашли поток и разрез для которых выполняется = С(А*) Учитывая, что выходящие дуги из А* пустые, то весь поток ср*(/}*} скатывается в z, т.е. y*(z) = С(А*).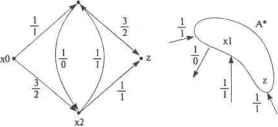

Рис. 6.26. Максимальный поток

Определение независимого множества вершин. Пусть граф Г= (X, U, Ф) - неориентированный и без петель. Множество / a U вершин называется независимым, если между любыми его вершинами нет соединяющих ребер. В зависимом множестве хотя бы две вершины соединены ребром. Множество Q полностью зависимое, если каждая пара его вершин соединена. Вершины графа, составляющие Q, образуют полный подграф.

Определение. Максимальное независимое множество есть независимое множество, которое становится зависимым после добавления к нему любой вершины. Заметим, что каждое независимое множество содержится в некотором максимальном независимом множестве. Максимальное число (5(7) вершин, составляющих независимое множество, называется числом (вершинной) независимости графа.

- Определение независимого множества ребер. Подобно независимым множествам вершин рассматриваются независимые множестваребер, состоящие из ребер, не имеющих общих вершин. Каждое независимое множество ребер содержится в некотором максимальном независимом множестве. Число ребер в максимальном независимом множестве называется числом реберной независимости $и(Г).

При представлении игр графами независимые множества вершин являются такими множествами позиций, что никакая из них не может быть достигнута из другой за один ход. Примером является задача о расположении максимального числа ферзей на шахматной доске так, чтобы ни один них не мог побить другого. Это максимальное число равно (3(7) = 8.

Утверждение 6.11.1. Независимое множество максимально тогда и только тогда, когда оно доминирующее, а значит, р(7) > 5(7)-число (вершинной) независимости не может быть меньше числа доминирования.

Доказательство. (=>) Если 7с U- максимальное независимое множество, то не может быть вершин k е 7, не соединенных с ребром, так как в противном случае множество fcu /также было бы независимым, но I- максимальное по условию. Отсюда 7 - доминирующее. (<=) Пусть 7- независимое доминирующее множество. Тогда никакое & нельзя перевести из 7 в /так, чтобы kvl осталось независимым, а значит, 7 - максимальное.

Определение. Клике есть полностью зависимое множество, которое теряет это свойство после добавления любой вершины. Клики графа представляют естественные группировки вершин в максимальные полные подграфы. Определение клик графа полезно в кластерном анализе в таких областях, как информационный поиск, в социолоши и др. В качестве примера на рис. 6.31 показан граф и его клики. 2 з 2 з

Замечание. Если предположить, что граф (X, U, простой, то полностью зависимые множества (клики) в Г становятся максимально независимыми множествами в дополнительном графе Г, верно и обратное.

При алгоритмическом подходе к выделению в графе применяют метод поиска с возвращением по специальному дереву поиска, устроенному следующим образом. Каждый узел в дереве поиска соответствует полному подграфу исходного графа, и каждое ребро дерева поиска соответствует вершине исходного дерева. Вершины (множества) дерева поиска определим рекурсивно. Корень дерева поиска - пустое начальное множество S = 0. Пусть теперь S - произвольная вершина дерева поиска какого-либо уровня. Тогда вершиной следующего уровня дерева поиска будет вершина Su {х}, еслих eS их смежна с каждой вершиной из S. В дереве поиска такие вершины S и S и {х} соединяются ребром, которое соответствует вершине х. На рис. 6.32 показаны некоторый граф Гидерево поиска Т, которое исследуется в процессе поиска с возвращениями клик графа полным перебором.

Заметим, что каждая клика порождается много раз: клика {1,2,3} порождается 3! раз, клики {3,4} {4,5} порождаются 2! раз. В общем случае клика размера к порождается к\ раз. Все тонкие ребра на рис. 6.32 исследования дерева поиска можно оборвать, они не приводят к новым кликам. Следующие два утверждения позволяют обрывать такие тонкие ребра (не исследовать их), обеспечивая целенаправленный проход по дереву поиска клик графа.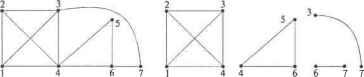

Рис. 6.31. Граф и его клики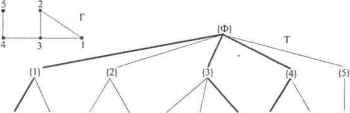

3} i2l) (23) (31} {3?} {34} {45} {43} {54}

{132} {123} {213} {231} {312} {321}

Рис. 6.32. Граф полный перебор дерева Т поиска клик

Утверждение 6.11.2. ПустьГ= (X, U, Ф) - исходный граф, S -узел в дереве поиска (S с X- подмножество вершин графа). Вершина Sдерева поиска уже обработана и первой вершиной, которую надо исследовать, является множество {х}, как на рис. 6.33, вершинах смежна с каждой вершиной из S. Пусть все поддеревья узла $ о {л; в дереве Гуже исследованы и порождены все клики, включающие $<и {х\ Тогда необходимо исследовать только те из вершин S kj {v,}. для которых

Утверждение 6.11.3. Пусть S - узел в дереве поиска Т, и пусть

S с S - предок h Т. Если все поддеревья узла S и{х} уже исследованы, что порождены все клики, включающие S то все неисследованные поддеревья с корнями можно

игнорировать.

Алгоритм 13 порождения клик графа представляет собой процедуру поиска с возвращением и является наиболее сложным из всех ранее рассмотренных алгоритмов. Рекурсивная процедура CLIQUE имеет два параметра: и D. Для рассматриваемого узла S

v z Aoj[a (рис. 6.33).

Рис. 6.33

Поддеревья

с корнями Su {v,\

(эти вершины смежны с 5)

поиска объединение представляет множество вершин,

смежных с каждой вершиной из S, т.е. NuD-множество вершин, которые могут выступать в качестве продолжения поиска клик из вершины S. Множество ./V состоит только из новых вершин, которые могут быть добавлены к Sв процессе поиска клик, т.е.

К- {х >~ ®\ix,s) e U\/seS с S ни одно из поддеревьев S {x} не исстЪчано).

Алгоритм 6.13. Порождение клик графа

S=0; {Начальнси вершина дерева поиска

N=X; D

Z=X;

CLIQUE(N, D, Z); {Рек\рсивнш проход по дереву поиска Procedure CL1QUE(N, D, Z)

if N и D = 0 then вывести S, которое является кликой else ifN*0then begin

x e N; {Исследоватьпервое поддерево) View(x); {Исследовать поддеревья) {Исследовапп оставшиеся поддеревья уровня) Z=Z\{x); Z=Z\Adj[x]; while Z*0do begin v <= Z;

View(\); {Исследовать поддеревья) Ze Z\{v); end; end; end;

Procedure View(v) {Исследовать поддеревья) N= N\{v); S=S{v);

CLIQUE{Nr,Adj[v], D n Adj[v], N rxAdj[v});

S=S\{v);

DP- U}:

end;

Процедура CLIQUE выбирает произвольную вершину x e N, удаляет ее из TV и исследует поддерево S= Su {х), обращаясь к процедуре View. Далее, согласно утверждениям 6.11.2и 6.11.3,при помощи процедуры исследуются только поддеревья S= 5и{у), где v е ТУ, v & Adj[x] что соответствует условию veZ. Множество

Zcoctomt из вершин одного уровня дерева, которые должны быть исследованы при рекурсивном проходе по дереву поиска, чтобы не потерять ни одной клики графа.

Второй параметр D процедуры CLIQUE представляет собой множество вершин, смежных со всеми вершинами из S, но таких, которые не надо добавлять к S на предмет продолжения формирования клик.

D = {х е X\\(x,s) е (7Vj eSu поддерево^ и{х} исследовалось для некоторых S с$1-

По алгоритму множество S с X является полным подграфом графа Г = (X, U, Ф) и Nu D - множество всех вершин, смежных с

каждой вершиной в S.

Множество S будет кликой тогда и только тогда, когда

Условие N= 0 и 0 обозначает, что все клики, включающие S, уже ранее порождались.

ПриЛЧ* 0 могут оставаться клики, включающие S, которые еще не порождались. Исследование таких поддеревьев S {х}, х в N необходимо продолжить.

Основные усилия алгоритма 6.13, порождения клик графа, направлены на поддержание множеств N к D, текущее состояние которых, согласно перечисленным выше условиям, предопределяет исследования по дереву поиска.

Программная реализация алгоритма порождения клик графа представлена в алгоритме 6.14 на Pascale, который близко соответствует множественному описанию алгоритма 6.13. Отметим, что в программной реализации передача множеств N, D, ZB качестве параметров процедур выполнена посредством указателей kN, nN, kl), nl), kZ, nZ, где kN, kl), &Z-указатели начала вершин в множествах, соответственно N, D, Z, a nN, nD, nZ - количество вершин в каждом из этих множеств.

Алгоритм 6.14. Программа порождения клик графа

Program PgmClique; {Выделение клик графа}

uses CRT, DOS;

Const

nVertex-100; {Максимальное количество вершин} nAdjacent-lOOO; {Максимальная длина списка смежности) Туре

TypeVertex=array (1. .nVertex] of Integer;

TypeAcijacent-array [i. .nAdjacent of Integer; Var

:Text; { Текстовый файл }

Integer; { Количество вершин в графе

:TypeAdjacent;{ Список смежности графа }

Fst Nbr

:TypeVertex; { Указатели вершин списка снепаости} :TypeVertex; { Количество вершин в списке смежности }

Vtx :TypeVertex; { Список вершин графа } S :TypeVertex; ( Список вершин формируемых клик } nS :Integer; { Количество вершин в списке S }

N :TypeVertex; { Список включаемых вершин

при поиске клик} [kN,nN - указатель начала и количества вершин в списке N) D :TypeVertex; {Список вершин с ранее найденными

кликами}

- указатель начала и количества вершин в списке

Z :TypeVertex; { Список не исследованных вершин }

- указатель начала и количества вершин в списке

Procedure PrintCliquo; FORWARD;

Procedure Subtract ( x:Integer; Var kZ,nZ:Integer ); FORWARD;

Procedure Var

teger; Var M:TypeVertex ); FORWARD;

Procedure View( v:Integer; VarkFpnN, kD,nD, kZ,nZ:Inte-

ger ); FORWARD;

Procedure Clique( Ш,nN,kD,nD,kZ,nZ:Integer ); FORWARD; Procedure Var yes -.Boolean ) ;

{ Переназначение меток вершин их порядковыми номерами

по списку смежности вершин графа } ( yes - признак правильной структуры списка смежности графа} Var

i,j,k :Integer;

begin

for i:=l to m do

for j:=l to Nbr[i] do begin yes:=FALSE;

for k:=l to m do

if Adj[Fst[i]+j]=vtx[k] then begin

yes:=TRUE;

Adj[Fst[i]+j]:=k;

break; end;

if not yes then exit; end;

end;

Procedure PrintClique;

( Печать вершин найденной клики } Var

i :Integer;

begin

for i:=l to nS do Write (f,Vtx[S [i]] : 3) ; WriteLn(f); end;

Procedure

Var kMw,nMw:Integer; Var M:TypeVertex ) ;

{ Формирование пересечения M*Adj [v] множеств M и Adj [v] } Var

i,j,k : Integer;

yes begin

{kMw - указатель начала вершин в множестве M*Adj[v]} {nMw - количество вершин в множестве M*Adj[v]} kMw:=kM+nM; nMw:= 0;

for i:=l to nM do

for j:=l to Nbr[v] do

if M[kM+i]=Adj[Fst[v]+j] then begin nMw:=nMw+l; M[kMw+nMw] :=M[kM+i] ; break; end;

end;

Procedure Subtract( x:Integer; Var kZ,nZ:Integer );

i(* Формирование разности множеств Z=Z\{x} и Z=Z\Adj[x] *)

i,j,k : Integer;

yes begin

(* Формирование Z=Z\{x} *) for i:=l to nZ do

if Z[kZ+i]=x then begin nZ:=nZ-l;

for k:=i to nZ do

break; end;

(* Формирование Z-ZXAdjtxl *)

for to Nbr [х] do

for i:=l to nZ do

if Z[kZ+i]=Adj[Fst[x]+j] then begin nZ:=nZ-l;

for k:=i to nZ do Z [kZ+k] :=Z [kZ + k + 1 ] ; break; end;

end;

Procedure Clique ( kN,nN,kD,nD,kZ,nS:Integer );

{ Процедура рекурсивного поиска клик графа } Var

i,j,x :integer;

begin

if (nN=0) and (nD=0) then {Клика найдена} PrintClique {Печать клики}

else if nN<>0 then begin {Продолжит! исследование

поддеревьев)

x:-N[kN+nN]; {Перебор с конца вершин множества N1

поддерево

Subtract(х,kZ,nZ); (* Z=Z\{x} и Z=Z\Adj[х] *)

while nZ<>0 do begin {Исследовать следующие

поддеревья уровня}

x:=Z[kZ+nZ];

View(x,kN,nN,kD,nD,kZ,nZ);

nZ:=nZ-l; (* Z = Z\(x:- *) end; end; end;

Procedure Var

{ Исследование поддеревьев следующего уровня } -Var

i,k -.Integer; kNw,nNw : Integer; kDw,nDw :Integer; kZw,nZw :Integer; begin

(* Формирование N=N\{v} *) for i:=l to nN do

if N[kN+i]=v then begin nN:=nN-l;

for k:=i to nN do

break; end;