d:=Dist[v];

for i:=2 to nX do

if d>Dist[X[i]] then begin v:=X[i]; d:=Dist[v]; end;

end;

Procedure newDist( v :Integer );{Обновить dist[] -

минимальные расстояния}

Var i :Integer; begin

for i:=l to nX do

if Dist[X[i]]>We[X[i] ,v] then begin Dist[X[i]] :=We[X[i],v] ; Prev[X[i]]:=v; end;

end;

Procedure

Var i,nStop,v :Integer; begin

nStop:=nX;

for i:=l to nX do X[ij :-=i; v:=l;

for to nX do begin

Distti]:=We[i,v]; Prev[i]:=v;

end;

nXo:=0; { Xo - пустое множество } nUo:=0; { Uo - пустое множество }

nXo:=nXo+l;

Xo[nXo]:=X[v]; {Xo=Xo+v - добавить вершину v к остову} X[v]:=X[nX]; nX:=nX-l; { X=X\v - удалить v из X }

Wt:=0;

while nxoonstop do begin minDist(v); nXo:=nXo+l;

Xo[nXo]:=v; {Xo=Xo+v - добавить вершину v к остову} for i:=l to nX do { X=X\v - удалить v из X }

if X[i]=v then begin X[i]:=X[nX]; break; end; nX:=nX-l; nUo:=nUo+l;

Uo [2*n0c-l] :=Prev [v] ; { Uo= Jo+ ( Prev [ v] , v ) -

добавить ребро к остову}

Uo[2*nUo]:=v;

Wt:=Wt+Dist[v]; { Обновить вес остовного дерева } newDist(v);

end;

end;

Var (Main)

i,j :Integer; begin {Main)

Assign(f,Near.in ) ;

Reset(f);{Файл открыт для чтения) Read(f,nXi; {Количестве вершин в графе) for i:=l to nX do begin for j : =i to nX do begin

Read(f,We[i,j]); { Ввод матрицы весов } if We[i,j]=0 then We[i,j]:=$7fff; {+бесконечность} We[j,i]:=We[i,j]; end; end;

Close(f);

Assign(f,Near.out);

открыт для

nUo:=0;{Выделение реберного списка графа для печати) for i:=l to nX do

for j:=i+l to nX do begin

if We[i,j]=$7fff then continue; nUo:=nUo+l; Uo[2*nUo-l]:=i; Uo[2*nUo]:=j; end;

WriteLn(f,nU =,nUo:3); WriteLn(f,nX =,nX:3);

i:=l to nX do Write

WriteLn(f); Write(f,ul =);

for i:=l to nUo do Write(f,Uo[2*i-1]:3);

WriteLn(f); Write(f,u2 =);

for i:=l to nUo do

WriteLn(f); Write(f,We =);

for i:=l to nUo do WriteLn (f); Ostov;

Write(f,uol=);

for to nUo do

WriteLn(f); Writeff,u62=);

for i:=l to nUo do

Write (f, Woe- ) ;

for i: = l to nUo do Write(f,We[Uo[2*i-l],Uo [2*i]I:3); WriteLn(f); Wt:=0;

for i: 1 to nUo do Wt: =Wt+We [Uo [2*i-l ] , Uo [2*i] ] ; Write(f,Bec=,Wt:3); Close (f); end.{Main}

Рассмотрим пример расчета по программе алгоритма построения минимального остовного дерева графа, изображенного на рис. 6.20. Исходные данные графа представляются матрицей весов его ребер в текстовом файле Near, in со следующей структурой:

в первой строке содержится количество вершин в графе;

в следующих п строках задаются верхние диагональные элементы (нулевые диагональные элементы включаются) строк матрицы! весов.

Результаты расчетов сохраняются в выходном файле Near.out

со следующей структурой:

= 12 nX = 7

Х = 1234567

ul =111223344556 u 2 = 267374757677 We = 20 23 1 15 4 3 9 17 16 28 25 36 uol= 1 7 7 3 4 1 uo2= 7 2 3 4 5 6 Woe= 1 4 9 3 17 23 Bec= 57.

Обозначения данных в файле Near, out соответствуют принятым обозначениям в файле Hungry.out при контрольном расчете остовного дерева по жадному алгоритму 6.8 (см.

6.9. Кратчайшие пути на графе

Рассматриваемый алгоритм определяет расстояния между вершинами в простом орграфе с неотрицательными весами. К таким орграфам сводятся многие типы графов. Если граф не является простым, его можно сделать таковым, отбрасывая все петли и заменяя каждое множество параллельных ребер кратчайшим ребром (ребром с наименьшим весом) из этого множества; каждое неориентированное ребро заменяется парой ориентированных ребер. Если граф не взвешен, то можно считать, что все ребра имеют один вес.

Пусть /= (X, U, Ф) - простой орграф, для каждого ребра и & U определен вес со (ы) > 0. Найдем кратчайший путь между выделенными вершинами Xq и z (рис. 6.21). Несуществующие ребра будем считать ребрами с бесконечными весами. Сумму весов ребер в пути будем называть весом или длиной пути. Обозначим щ= Ш(И) - вес ребра и = (xt, х,). Алгоритм поиска кратчайшего пути, начиная из вершины просматривает граф в ширину, помечая вершины значениями-метками их расстояний отд^. Метки могут быть временные и окончательные. Временная метка вершины х - это минимальное расстояние от х0 до когда в определении пути на графе учитываются не все маршруты из щ в Xj. Окончательная метка Xj - это минимальное расстояние на графе х0 до Xj. Таким образом, в каждый момент времени работы алгоритма некоторые вершины будут иметь окончательные метки, а остальная их часть - временные. Алгоритм заканчивается, когда вершина z получает окончательную метку, т.е. расстояние от Xq до z.

Вначале вершине JCo присваивается окончательная метка 0 (нулевое расстояние до самой себя), а каждой из остальных - 1 вершин присваивается временная метка да (бесконечность). На каждом шаге одной вершине с временной меткой присваивается окончательная и поиск продолжается дальше. На каждом шаге метки меняются следующим образом.

1. Каждой вершине Xj, не имеющей окончательной метки, присваивается новая временная метка - наименьшая из ее временной и числа (vv,( + окончательная метка л/), где - вершина, которой присвоена окончательная метка на предыдущем шаге.

2. Определяется наименьшая из всех временных меток, которая и

становится окончательной меткой своей вершины. В случае равенства меток выбирается любая из них.

Циклический процесс п. 1+п.2 продолжается до тех пор, пока вершина z не получит окончательной метки. Легко видеть, что окончательная метка каждой вершины - это кратчайшее расстояние от этой вершины до начала х().

Рассмотрим пример поиска кратчайшего пути на графе, представленном на рис.

Рис. 6.21. Простой взвешенный орграф

Процесс назначения меток вершинам графа на каждом шаге удобно представить в виде следующей таблицы.

Квадратами выделены окончательные метки, т.е. расстояния от них до х0. По такой таблице легко восстановить путь перемещения от z к Xq, который отмечен ломаной кривой.

Реализация рассмотренной схемы поиска кратчайшего пути представлена в алгоритме где граф (X, U, Ф) представляется матрицей весов We = [w,y], веса несуществующих ребер полагаются равными +ао. Вектор Mark[x] меток вершин устанавливает принадлежность вершиных Е Л' постоянной (TRUE) или временной (FALSE) метке. Вектор Dist[x] в алгоритме фиксирует текущие значения меток вершин. Вектор Prev[x] позволяет восстановить в обратной последовательности вершины кратчайшего пути.

Алгоритм 6.11. Алгоритм кратчайшего пути на орграфе

forx е Xdo begin Mark[x] = FALSE; DistfxJ = oo; end; y=xQ;

Mark[xo\ = TRUE; Distil] = 0;

while not Mark[z] do begin forx e Xdo

if not Mark[x] and dist[x] > dist\y] + w[y, zj then begin distfx] = dist[y] + w\y,x]; prev[x] = y;

end;

{Поиск новой вершины у е Xс минимальной временной меткой) dist\y] = min dist\x\

xeJCand Mark[x\= FALSE

Mark[v = TRUE; end.

Prev[x] указывает на вершину с окончательной меткой, ближайшую к вершине х. Последовательность вершин кратчайшего пути будет имеет следующий вид:

z, prev[z], prev[prev[z]],prev[prev[prev[z]][ ... , х0,

а значение Dist[z] составит длину пути из л0 в Очередная новая вершина, претендующая на постоянную метку, обозначается через у.

Сложность алгоритма, Алгоритм обращаетсяк телу цикла while не более \Х\ 1 раз. и число операций, требующихся при каждом таком обращении, равно 0([А]). Тогда сложность алгоритма составит 0(\Х\ ).

Интересно заметить, что если требуется найти длины кратчайших путей от х0 до всех вершин графа, то в алгоритме условие цикла while not Mark[z] do begin надо заменить на условие while v not Mark[x] do begin. При этом сложность алгоритма останется

прежней.

Программная реализация алгоритма поиска кратчайшего пути представлена в алгоритме 6.12 на Pascale, который близко соответствует множественному описанию алгоритма

Алгоритм 6.12. Программа кратчайшего пути на орграфе

Program Short; (Кратчайшие пути на графе)

uses CRT,DOS;

Const

nVertex=50; {Максимальное количество вершин) Type

TypeMark=array[0..nVertex] of Boolean; TypeDist=array[0..nVertex] of Longlnt; TypePrev=array[0..nVertex] of Integer; TypeWeight=array[0..nVertex,0..nVertex] of Integer; Var

{ Текстовый файл } { Количество вершин в графе }

nX Mark Dist

:Text; : Integer; :TypeMark; :TypeDist;

:TypePrev; :TypeWeight; :Integer; :Integer;

{Признаку временных и постоянных меток} { Значения текущих меток вершин (расстояния)}

{ Указателв на ближайшую вершину } Матрица весов ребер графа } Вершина начала пути } Вершина конца пути }

: Integer; {Последняя вершина с постоянной ыг-гксО j

Prev We хО z у

i,j,x :Integer; weight :Longlnt; begin

Assign(f,Short.in) ; Reset (f) ;{Файл открыт для чтения} {Ввод исходных данных)

вершина вершина

вершин в

пХ:=пХ-1; (* Х={0,1,2,. . . , пХ} - множество вершин

for i:=0 to nX do begin for j:=0 to nX do begin

{ Ввод матрицы весов } if We[i,j]=0 then We[i,j]:=$7fff; {+бесконечность}

end;

end;

Close(f);

Assign(f, Short.out);

открыт для

for х:=0 to nX do begin

Mark[x]:=FALSE;

Dist[x]:=$7fffffff; end;

у:=хО; {Последняявершина с постоянной меткой) Mark[у]:=TRUE; Dist[у]:=0;

while not Mark[z] do begin

{Обновить временные метки)

for х:=0 to nX do if not Mark[x] and

( Dist[x]>Dist[y]+We[y,x] ) then begin

Dist[x]:=Dist[y]+We[y,x];

Prev[x]:=y; end;

{Поиск вершины с минимальной временной меткой) weight:=$7fffffff;

for x:=0 to nX do if not Markfx] then

if weight>Dist[x] then begin

weight:=Dist[x];

y:=x; end;

Markfy]:=TRUE; end;

Write(f,Вершины пути=);

x:=z;

while xoxO do begin Write(f,x:2); x:=Prev[x];

end;

WriteLn(f,x:2);

WriteLn(f, Длина пути= \Dist[z]); Close (f); end.

Рассмотрим пример расчета по программе алгоритма поиска кратчайшего пути на графе, показанном на рис. 6.21. Исходные данные графа представляются матрицей весов его ребер в текстовом файле Short.in со следующей структурой:

в первой строке определяется номер начальной вершины л^;

во второй строке определяется номер конечной вершины пути z,

в третьей строке указывается количество пХвершин в графе;

в следующих определяются строки матрицы весов графа.

о

б

00 000

0 10

Результаты расчетов сохраняются в выходном файле Short.out со следующей структурой:

Вершины пути= Длина пути= 11.

6.10. Потоки в сетях

Определение. Транспортной сетью называется связный ориентированный граф без петель Г= (X, U, Ф) с выделенной парой вершин ;с0 и z (рис. 6.22). Вершина х0 - начало транспортной сети, из которой дуги только выходят. Вершина z - конец транспортной сети, в которую дуги только входят. На множестве дуг и Uзадана целочисленная функция с(и) > О, где с(и) - пропускная способность дуги.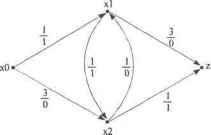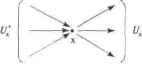

Рис. 6.22. Транспортная сеть

Определение. Потоком по транспортной сети называется целочисленная функция 0 , заданная на множестве дуг и и обладающая следующими свойствами:

VueU(tfu)uC(u) и £<р(и) = £ф(и), (6.10.1)

где х - внутренняя вершина графа, т.е. х*х$, х

- множество дуг, заходящих в вершину х;

- множество дуг, выходящих из вершины х (рис. 6.22).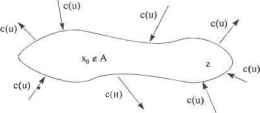

Рис. 6.23. Разрез транспортной сети

С'!, i = и) - называется мощностью разреза. Это максимально ueUA возможный поток, входящий в А по дугам разреза.

ф(/1) = ф(н) - поток, входящий в А по дугам разреза. Ясно, что и<=и+А у(А) < С(А), так как V е U ф(и) < с(и).

Утверждение 6.10.2. ф) < С(А).

Действительно, из рис. 6.23 видно, что не весь поток, входящий в А, скатывается в z. Часть потока может выходить из А. Значит, но тогда и

На рис. 6.22 напротив каждой дуги стоит дробь, числитель которой - пропускная способность дуги, знаменатель - поток по дуге. Свойство 1) утверждает, что поток, входящий в вершину, равен выходящему потоку (поток в вершинах не скапливается). Обозначим

где поток, входящий в вершину z\ ф(х0) - поток, выходящий из вершины х0.

Утверждение 6.10.1. ф(г) =ф().

Действительно, сумма ]£[ £ф(н)- ]Гф(и)]=0, таккак V € U

хеХ uel/* uid/~

величина ф(н) суммируется дважды - со знаками + и -. Здесь

1ГЕфИ-Х>( И= X Цф< )-1Ф< )1+Ф(г)-ф(х0)=0,

xsXu&t < &i хеХ\{хал) иеУ* ltd/:

где первая часть выражения равна нулю вследствие 6.10.1,

Определение разреза. Пусть А сХ - множество вершин транспортной сети: л:0 g A, z е А. Обозначим через £Г$ множество дуг, входящих в А. Это множество дуг будем называть разрезом

транспортной сети.