Утверждение 1. Дерево с и вершинами содержит - 1 ребро. Доказательство. Доказательство проведем по индукции числа

вершин. Заметим, что в дереве найдется вершина, степень которой равна единице (висячая вершина). Действительно, в противном случае, если степени вершин 2, можно построить цикл, что противоречило бы определению дерева. Цикл строится следующим образом. Выполним проход по ребрам графа, начиная с произвольной вершины. Так как степени 2, то, попав в вершину первый раз, можно всегда из нее выйти. Исходный граф - конечный и связный. наступит момент, когда вновь попадем в

пройденную уже вершину, что доказывает существование цикла.

Условие индукции для п = 2 выполняется, дерево с двумя вершинами содержит одно ребро. Предположим теперь, что утверждение выполняется для деревьев, число вершин у которых меньше п. Рассмотрим дерево с п вершинами. Удалим из этого дерева висячую вершину и инцидентное ей ребро. Очевидно, что оставшийся граф будет связным и без циклов, т.е. будет деревом с п - 1 вершиной. Тогда по предположению индукции оставшаяся часть графа содержит п - 2 ребра, а значит, исходное дерево должно иметь их п - 1.

Практическую значимость деревьев дает популярная

форма задачи Юли. Необходимо соединить п городов железнодорожными линиями так, чтобы не строить лишних дорог. Известна стоимость строительства для каждой пары городов. Какова должна быть сеть дорог, соединяющая все города и имеющая минимальную возможную стоимость? Аналогичные вопросы возникают при проектировании линий электропередач, сетей ЭВМ и др.

В терминах теории графов задачу можно сформулировать следующим образом. Рассмотрим граф Г= (X, U, Ф), где X- города, дороги. Каждому ребру и & (/назначим вес о(м) - стоимость строительства дороги и. Задача состоит в том, чтобы построить связный граф Г,0=(Х, U0, Ф), содержащий все вершины, с минимальным весом , что - дерево,

в противном случае можно было бы удалить одно ребро, не нарушая связности Г0и уменьшая сумму весов его ребер.

Определение. Минимальным остовным деревом (лесом) называется остовное дерево (лес) с минимальным общим весом его

6.8.1. Жадный алгоритм построения минимального остовного дерева

Минимум остовныхдеревьев графа Г = (X, U, Ф) можно применяя процедуру исследования ребер в порядке возрастания их весов. Другими словами, на каждом шаге выбирается новое ребро с наименьшим весом, не образующее циклов с уже выбранными ребрами. Процесс продолжается до тех пор, пока не будет выбрано \Ж\- 1 ребро. Рассмотренная процедура называется жадным алгоритмом.

Реализация данной схемы может быть выполнена следующим образом. Для каждой вершиныХ= {хьх2,..., хп} графа Г= (X, U, Ф) формируются начальные тривиальные компоненты связности

= (ВД, Ф), гдеЛ = {*,-}, Ц =0,X,nXj=0% /*/ V -\Ja,. i-.-. i, 2,..., X Компоненты деревьями, объединение Т --{JT,

которых дает начальное приближение строящегося остовного де-реваГ0=(Х, Uо, Ф).

Включение в строящееся остовное дерево Г0 выбранного ребра на очередном шаге жадного алгоритма выполняется слиянием 7} = 7} u T,(Xj = Л/-..л1и Ц = 11,; Щ двух компонент 7) и которым принадлежит по вершине нового ребра, и включением самого ребра в объединенное множество Ц=ЦиЦ ребер. Процесс роста объединения Т компонент к основному дереву 0 = (X, U0, Ф)

продолжаем до тех пор, пока не будет включено - 1ребро.

Справедливость жадного алгоритма является следствием следующих двух лемм.

Лемма 6.8.1. Пусть Г = (X, U, Ф) - связный неориентированный граф и Гс = (X, U0, Ф) - произвольное остовное дерево для него. Тогда:

1) V . единственная между ними цепь в Г0;

2) если к добавить ребро из U\ U0, то возникнет ровно один цикл.

Доказательство. Утверждение 1 верно, т.к. в противном случае в существовал бы что противоречит дереву Утвержде-

ние 2 верно, поскольку между вершинами добавляемого ребра уже есть одна цепь, а значит, возникнет один цикл.

Лемма 6.8.2. ПустьГ= (X, U, Ф) - связный неориентированный граф, для каждого ребра и U определен вес со (и), и Tj= (Xj, Uit Ф) - компоненты связности жадного алгоритма, объединение которых Т = [J 7} согласно алгоритму, растет к

осшшюму дереву = (Х,и0,Ф), где = 1,2,..., к и к > Пусть следующим найденным для включения ребром является ребро Е = (х, у) наименьшего веса из оставшихся U \ у £7,- и пусть х е Х\

шу£Жр Тогда найдется остовное дерево Г0дляГ=(Х, U, Ф>, содержащее ребра\JU, u{E}, вес которого не больше любого

г

другого остовного дерева, содержащего ребра у

Доказательство. Допустим противное. Пусть существует остовное дерево =(Х,и'0,Ф) дл Г, содержащее и не содер-

жащее ребра Е, вес которого меньше весалюбого остовного дерева для Г, содержащего у По 1 при

добавлении Е к образуется цикл. Этот цикл

должен содержать такое ребро от-

личное от Е, что х'е Х^ и .rV. Ху, т.к. цикл входит в по ребру (х, у) и у то он должен и выйти из Uy (рис. 6.19). Из условия следует, что Рис. 6.19 вессо(Е) < со(е),таккаку(7; с c70H(Jt7,- с U0k

ребро Е выбиралось минимальным весом из оставшихся ребер

U\Y Uj без образования циклов, в противном же случае выбор должен был бы пасть на Е т.к. оно тоже не образует циклов сyUj.

Рассмотрим граф Г0 = (Х, U0, Ф), образованный добавлением Е к Гс и удалением Е из Г'0. В нет циклов, так как единственный

цикл разорван удалением ребра Е . остался так как

осталась цепь между*иу. Таким образом, - остовное дерево. Учитывая, чтосо(Б) < со (в), то вес дерева Г0 не больше веса Г'0. Остовное дерево с содержит и Е, а это противоречит предположению минимальности что доказывает справедливость жадного алгоритма.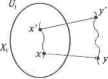

Реализация жадной схемы формирования остовного дерева представлена в алгоритме 6.7. Используемые при его описании обозначения соответствуют тому, что вводилось при обосновании жадной схемы. Вектор Магк[х] меток вершин х е X графа поддерживает их принадлежность компонентам связности из которых формируется реберный список остовного дерева. Начальные величины устанавливаются равными порядковым номерам соответствующих вершин е X. Далее значения МагЦх корректируются по мере слияния компонент сохраняя соответствие принадлежности им вершин. Исходный граф задается реберным списком U, выходное остовное дерево также формируется реберным списком Щ.

Алгоритм 6.7. Жадный алгоритм минимального остовного дерева forXj е Xdo Магк[х,]= /;

Sort(U); {Сортировке списка ребер по их весам)

и0= 0;

while \Uq\<\X\-\ do begin

(х, у) е U; {Ребре с min весом из оставшихся) ifMark[x}t Mark[y] then begin

U0= U0 u \(x, у)}; {Включить ребре в остовное дерево) Z = Mark\y\, {Слияние UxuUy) for v 6 Xdo ifMark[vy= z then Mark[v] = Mark[x]\

end;

U= Щ(х,у)}; {Удалитъребро с min весом из списка)

end;

Сложность жадного алгоритма. Жадный алгоритм требует предварительной сортировки ребер по их весам. Стандартные методы сортировки имеют сложность 0{\U\). Сложность алгоритма 6.7 помимо сложности сортировки зависит от сложности реализации слияния подмножеств и If Сложность данной операции при полном переборе вершин данных подмножеств (как представлено в алгоритме 6.7) составляет 0(pf 2). Значит, сложность жадно го алгоритма 0(А']2) + 117 2). Программная реализация жадного алгоритма представлена в

алгоритме 6.8, который близко соответствует множественному

описанию соответствующего алгоритма 6.7.

Алгоритм 6.8. Программа жадного алгоритма

Program дерево. Жадный алгоритм)

uses CRT,DOS;

Const

nVertex=5D; {Максимальное количество вершин) nRib=1000; {Максимальна; количество ребер'1 Туре

TypeVertex=array[1..nVertex] of Integer; TypeRib=array[1..nRib] of Integer; Var

Procedure {Переназначение меток вершин }

i,j,m :Integer;

begin

for i:=l to 2*nU do Uo[i]:=l; for i:=l to 2*nU do

for j:=1-1-1 to 2*nU do if Uo[j]=l then if U[jl=U[i] then Uotj]:=0; nX:=0;

for i:=l to 2*nU do if Uo[i]=l then begin nX:=nX+l; X[nX] :=U[i] ; end;

for to do

for m:=l to nX do

if U[i]=X[m] then begin U[i]:=m; break; end;

end;

Procedure Sort; { Сортировка списка ребер по их весам }

i,j,k :Integer; w :Integer;

begin

for i:=l to nU do for j:=1 to nU-i do

if We[j]>We[j+l] then begin

w:=We[j]; We [ j] :=We[j+1] ; We[j+1]:=w; w:=U[2*j-l]; U[2*j-1] :=U[2*( j+1)-1] ; D[2*(j+1)-1] :=w;

w:=U[2*j] ; U[2*j ] :=U[2*(j+D ] ; U[2*( j+1) ] :=w;

end;

end;

Procedure { Строим минимальное остовное дерево }

i,х,у,z : Integer;

sU Integer,-

begin

for i : =1 to nX do Mark[i] :=i;

Sort; {Сортировка ребер по весу)

nUo:=0; {Пустое множество Uo}

sU:=l; {Начальное ребро в сортированном U)

while nUo<nX-l do begin

x:=U[2*sU}; (Выбор нового ребра из списка)

y:=U[2*sU-l] ;

if Mark [x] OMark [у] then begin nUo:=nUo+l;

ребро в остовное z:=Mark[y]; {Слияние Ux и Uy} for i:=l to nX do if Mark[i]=z then Kark[i]:=Mark[x]; end;

ребро из

end;

end;

Var {Main}

i,j : Integer; begin {Main}

Assign(f,Hungry.in);

Reset (f) ; {Файх открыт для чтения}

Road(f,nU); {Количестве ребер з реберном списке графа} for to nU do Read (f, U [2*i-1 j ) ; { Первые вершины

ребер }

for i:=l to nU do Read (f, U [2*i] ) ; { Вторые вершины

for i:=l to nU do Read (f,We[i] ) ; { Веса ребер } Close (f) ;

Assign(f, Hungry.out);

открыт для

Init;

Sort

WriteLnff, nU = ,nU:3) ; WriteLn(f , nX = ,nX:3);

Write (f,X =);for i:=l to nX do Write (f,X[i] :3) ;

WriteLn(f); Write (f,ul =);

for i:=l to nU do Write(f,x[u[2*i-l] ] :3) ;

WriteLn(f); Write(f,u2 =);

for i:=l to nU do Write (f,x[u[2*i] ] :3) ;

WriteLn(f); Write(f,We =);

for i:=l to nU do Write (f,We [i] : 3) ;WriteLn(f) ;

Ostov;

Write(f,uol=);

for i:=l to nUo do Write(f,X[U[2*Uo[i]-1J] :3) ; WriteLn(f); Write(f,uo2=);

for i:=l to nUo do Write (f, X [U [2*Uo [i] ] ] : 3 ) ; WriteLn(f); Write (f,Woe=);

for i:=l to nUo do Write(f,We[Uo[i]]:3); WriteLn(f); Wt:=0;

for i:=l to nUo do Wt:=Wt+We[Uo[i]]; Write(f,Bec=,Wt:3); Close (f); end. {Main}

Рассмотрим пример построения минимального дере-

ва графа, изображенного на рис. 6.20, по программе алгоритма 6.8.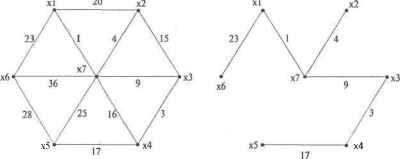

Рис. 6. 20. Пример расчета остовного дерева

Для программы этого алгоритма исходные данные графа на рис. 6.20 задаются реберным списком в текстовом файле Hung-ry.in со следующей структурой:

в первой строке файла содержится количество ребер в списке

(12);

во второй и третьей строках указываютсяребра своими вершинами: одна вершина во второй строке, другая вершина ребра в

третьей строке;

в четвертой строке располагаются значения весов соответствующих ребер.

777777 123456 123456234561

1 4 9 16 25 36 20 15 3 17 28 23

Результаты расчетов сохраняются в выходном файле Hung-ry.out со следующей структурой:

nU = 12 пХ = 7

Х = 7123456

ul = 737727416757 u2 =142334521566 We = 1 3 4 9 15 16 17 20 23 25 28 36 uol= 7 3 7 7 4 6 uo2= 1 4 2 3 5 1 Woe = 1 3 4 9 17 23 Bec= 57.

Обозначения данных в файле Hungry.out: nU - число ребер в графе; пХ - число вершин в графе; X - список вершин графа; (ul, u2) - сортированный список ребер графа; We - веса ребер согласно их сортировке; (но 1, uo2) - ребра остовного дерева; Woe - веса ребер остовного дерева; Вес - сумма весов ребер остовного дерева.

6.8.2. Алгоритм ближайшего соседа построения остовного дерева

Данный метод построения минимального остовного дерева не требует ни сортировки, ни проверки на цикличность на каждом шаге.

1. Построение остовного дерева Г0 начинается с произвольной вершины

2. Затем среди ребер, инцидентных хь выбираем ребро (*i,JC2) с наименьшим весом и включаем его в дерево

3. Повторяя процесс, выполняем поиск наименьшего по весу ребра, соединяющего вершины и с некоторой другой вершиной графа х3.

4. Процесс включения ребер продолжаем до тех пор, пока все вершины исходного графа Г не будут включены в дерево Построенное дерево будет минимальным остовным. Доказательство того, что последовательность шагов -4 приводит к построению минимального остовного дерева, аналогично доказательству для жадного алгоритма. Реализация схемы ближайшего соседа формирования остовного дерева выполнена в алгоритме 6.9, где исходный граф Г= (X, U, Ф) представляется матрицей весов [vfy], веса несуществующих ребер полагаются равными +=о. Под весами ребер понимаются их длины. Остовное дерево Г0 = (Х0, U0, Ф) формируется посредством реберного списка Uc и списка вершин В качестве меток вершин устанавливаются их порядковые номера Х= {1,2,..., п]. Для каждой вершины х е Аграфа, еще не включенной в остовное дерево, поддерживается минимальное расстояние до множества ранее включенных вершин вЛу. Это осуществляется с помощью двух векторов dist[x]

где равно минимальному расстоянию е

вершины prevfx] е Х0. Обновление значений векторов dist[x] и prev[x] выполняется на каждом шаге алгоритма при пополнении Х0 новой вершиной.

Сложность алгоритма ближайшего соседа. Сложность алгоритма определяется двумя вложенными циклами по числу вершин. В каждом из циклов выполняется константное число операций. Следовательно, сложность составляет 6>(.\f).

Алгоритм 6.9. Алгоритм ближайшего соседа для остовного дерева

Х= {1, 2,..., п}; {Меткивершин графа} пХ= \Х\; {Количество вершин в графе} v = вершина v е

Хс - Mi {Вершинь остовного дерева] X=X\{v); {Удалить v изХ} Uc = 0; {Ребре остовного дерева] остовного forx е X do begin

disl[x = от х до v е Х0]

prevfx] = v; {Ребро (v, х), длина которого dist[x]} end;

while \Х0\* nX dobegin

distfv] = min dist[x]; { v e Х- вершина для включения]

6.8. деревья.

Х0 = Х0 и {v}; {Добавить вершину) X=X\{v); {Удалить вершину) U0= U0u{prev[v], v}; {Добавитьребро) WT= WT+ dist[v]; {Поправить вес дерева] {Поправить dist[x] - вектор расстояний] forxe Xdoifdist[xP We[v,x] then begin dist[x = prev[x] = v; end, end.

Программная реализация алгоритма ближайшего соседа представлена в алгоритме который близко соответствует множественному описанию соответствующего алгоритма 6.9.

Алгоритм 6.10. Программа алгоритма ближайшего соседа

Program {Остовное дерево.

Метод ближайшего соседа}

uses CRT,DOS; Const

nVertex=50; {Максимальное количество вершин} nRib=1000; {Максимальное количество ребер} Туре

TypeVertex=array[l..nVertex] of Integer; TypeRib=array[1..nRib] of Integer;

TypeWeight=array[l..nVertex,1..nVertex] of Integer;

f :Text; { Текстовый файл }

nX :lnteqer; { Количество вершин в графе }

{ Количество вершин в остовном дереве}

{ Количество ребер в остовном дереве }

nXo nUo

Prev

Dist

:Text; :Integer; :Integer; :Integer; :TypeVertex; :TypeVertex; :TypeRib; :TypeVertex; :TypeRib; :TypeWeight; :Longlnt;

{ Список вершин графа }

{ Список вершин остовного дерева }

{ Ребра остовного дерева }

{ Список ближайших вершин }

{ Расстояния до ближайших вершин }

{ Матрица весов ребер графа }

{ Вес минимального остовного дерева

Procedure Var v

Var i,d :Integer;

begin

v:=X[l];

соседа}

ближайшего