TypeVertex=array[l..nvertex} of Integer; TypeAdjacent=array[l..nAdjacent] of Integer;

Procedure Var yes :Boolean );

{ Переназначение меток вершин }

{ их порядковыми номерами в списке смежности } { yes - признак правильной структуры списка смежности } Var

i,j,m :Integer;

begin

for i:=l to n do

for j:=l to Nbr[i] do begin yes:=FALSE; for m: - = 1 to n do

if Adj[Fst[i]+j]=Vtx[m] then begin yes:=TRUE; Adj [Fst [i]+j] :=m; break-end;

if not yes then exit; end;

end;

Procedure

i,v : Integer; begin

Mark[x]:=count;

Алгоритм 6.4. Программа выделения связных компонент неориентированного графа Program {Выделение компонент

связности графа}

uses CRT,DOS; Const

nVertex-100; {Максимальное количество вершин} nAdjacent=1000; {Максимальная длина списка смежности}

for i:=l to Nbr[x] do begin v:=Adj[Fst[x]+i];

if then

end end;

Procedure Connect; (Выделение компонент связности}

v,count :Integer;

begin

for v:=l to n do Markfv]:=0;

count:=0; {Номер компоненты связности}

for v:=l to n do begin

if Mark[v]=0 then begin count:=count+l; Component(v,count) ;

end; end;

end;

Var {Main)

i, j :Integer; yes :Boolean; begin {Main}

Assign(f,Connect.in ) ; Reset (f) ; (Фай, открыт для чтения) { Ввод списка смежности } Read(f,n); {Количестве строк в списке) Fst[1]:=0; {Указатель начала первой строки списка) for i: =1 to n do begin

Read(f,Vtx[i]); { Метка вершины)

Read{f,Nbr[i]); { Количество вершин в списке)

for j:=l to Nbrfi] do Read (f, Adj [ Fst [ i]+j ]) ;

{ Список смежных вершин) Fst [i+1] :=Fst[i]+Nbr[i];{Указатель начала следующей

строки в

end;

Close(f);

Assign(f,Connect.out);

Rewrite(f); {Файл открыт для записи) Init(yes);

if not yes then begin

WriteLn(f, Плохая структура смежности графа!);

Close(f);

exit ; end;

5-2697

Connect;

for i:=l to n do Write(f,Vtx[i]:3); Writeln(f); for i:=l to n do Write(f,Mark[i]:3) ; Close (f) ; end. {Main}

6.7. Эйлеровы графы

Классической в теории графов является следующая задача. Имеются два острова, соединенньгх семью мостами с берегами реки и друг с другом, как показано на рис. 6.15. Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя по каждому мосту один раз, вернуться обратно. Решение этой задачи сводится к нахождению некоторого специального маршрута на графе.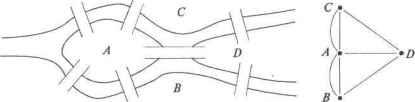

Рис. 6.15. План расположения мостов и соответствующий ему мультиграф

Определение. Пусть/= (X, Ф) - неориентированный псевдограф. Цепь в Г называется эйлеровой, если она проходит по одному разу через каждое ребро псевдографа Г. Такой граф называется эйлеровым. Замкнутая эйлерова цепь называется

эйлеровым циклом.

Поставим в соответствие плану расположения суши и мостов, приведенному на рис. мультиграф на рис. в котором

каждой части суши соответствует вершина, а каждому мосту - ребро, соединяющее соответствующие вершины. Теперь задача звучит так: найти эйлерову цепь (цикл) в мультиграфе. Решение этой задачи было дано Л. Эйлером.

Теорема Л. Эйлера. Эйлерова цепь в псевдографе Г= (X, U, Ф) существует тогда и только тогда, когда выполняются следующие условия:

1. Граф связный;

2. Степени внутренних вершин четные (внутренние вершины не являются началом и концом

3. Если вершины а и Ъ являются началом и концом цепи и а Ь, то степени их нечетные;

4. Если вершины а и b являются началом и концом цепи и a =b, то степени их четные.

Доказательство. (=>) Дано, что существует эйлерова цепь auhx2u2...xnunb, где а, b, xs е X, и, е U, в которрй содержатся все ребра по одному разу. Такая цепь включает все вершины графа, если граф не содержит изолированных вершин. Докажем условия 1) по данной цепи из любой вершины можно попасть в любую другую, значит, граф связный; 2) каждая тройка цепи Щ хх(щ привносит вершине л:,- степень два, а так как все ребра и, в цепи различные, то степени внутренних вершин четные; 3) и 4) доказательства повторяют доказательство пункта 2.

( =) Даны условия 1-4. Построим эйлерову цепь. Предварительно приведем условие 3 к условию 4 включением в граф фиктивного ребра которым свяжем вершины а и Теперь и в случае 3 все вершины будут иметь четную степень. Пусть А е X- произвольная вершина (рис. 6.16). Из нее будем строить цепь, выбирая в качестве продолжения пути ребро, которое еще не пройдено. Эта цепь (цикл может закончиться только в вершине А, та к как, при входе в любую другую вершину, всегда существует ребро, по которому можно выйти из нее (степени вершин

Возможны два случая: 1) построенный цикл Гг содержит все ребра графа, тогда теорема доказана; 2) содержит не все ребра графа. Во втором случае рассмотрим граф Г \ /полученный удалением из всех ребер, входящих в . Граф Г \ вновь содержит вершины только с четными степенями (у каждой вершины удалили по четному числу Так как Г- связный граф, то существует вершина в , инцидентная ребру из Г \Гу. Пусть это вершина В X. Построим из нее цикл так же, как строили цикл I]. Построим общий цикл из и так, как это сделано на рис. Для вновь проверяем рассмотренные выше два случая, как для /

Рис. 6.16. Объединение двух циклов в один цикл

Процесс расширения продолжаем до тех пор, пока не будут включены все ребра графа в один цикл: Аи{х2...аи*Ь...и„А. Разрывая данный цикл по ребру и*, получим эйлерову цепь flwi/2.,./ w £, где tj s X, w,e U.

Конструкта вный характер доказательства теоремы позволяет на формальном уровне в алгоритме 6.5 записать рассмотренный поиск эйлеровой цепи. Исходный граф представлен своей структурой смежностиЛфх] где - множество вершин, смежных е X.

Результирующая эйлерова цепь формируется в множестве Z.

Алгоритм 6.5. Алгоритм поиска эйлеровой цепи графа

3v is X; {Вершина начала эйлеровой цепи)

Z- М; {Начало строящейся эйлеровой цепи}

R = 0; {Частныйрасширяющийся цикл эйлеровой цепи}

repeat

Cycle(v, R);

Z=ZR, {Объединениециклов в один цикл) until Not 3ve Z \AdJM\> 0

Procedure Cycle(v, R)

R= {v}; {Построениеотдельного цикла эйлеровой цепи) repeat

w = Adj[v]; R=Rv{w};

Adj[v]=Adj[v]\ {w}; {Удалить пройденное ребро (v, w) } . ifv*wthen Adj[w] = Adj[w]\ {v}; {Удалитьpe6po(v, w) }

v =w;

until Not \Adj[v]\> 0; {Пока все ребра не пройдены} end;

Частные же циклы, расширяющие Z, представляются множеством R. Ребра, включенные в частный цикл R (а значит, и в Z), удаляются как пройденные из структуры смежности Adj[x] (из графа). Формирование расширяющих циклов R осуществляется до тех пор, пока структура смежности графа содержит хотя бы

одно ребро.

Сложность алгоритма поиска эйлеровой цепи. Число обращений к процедуре Cycle не более, чем число вершин При каждом обращении количество производимых действий пропорционально числу ребер, входящих в выделенный цикл. Сложность суммарной работы процедуры Cycle пропорциона-

льна количеству ребер £/вграфе. Поэтому сложность выделения эйлеровой цепи составляет 0(\Х\ + \U\). Программная реализация поиска эйлеровой цепи представлена в алгоритме 6.6, который соответствует множественному описанию соответствующего алгоритма 6.5.

Алгоритм 6.6. Программе поиска эшеровой цепи графа

Program EilerWay; {Эйлерова цепь в псевдографе}

uses CRT,DOS;

Const

nVertex=100; {Максимальное количество вершин) nAdjacent 1000; /Максимальная длина списка смежности) Туре

TypeVertex=array[1..nVertex] of Integer; TypeAdjacent=array[1..nAdjacent] of Integer;

f :Text; { Текстовый файл }

ks : Integer; { Начальная вершина эйлеровой цепи }

n :Integer; { Количество вершин }

Adj :TypeAdjacent; { Список смежности графа }

Fst :TypeVertex; { Указатели вершин списка смежности)

Nbr :TypeVertex; { Количество вершин в списке

смежности } Vtx :TypeVertex; { Список вершин графа } Deg :TypeVertex; { Степени вершин графа } kz :Integer; { Количество вершин в эйлеровой цепи) z :TypeAdjacent;{ Последовательность вершин

эйлеровой цепи } г :TypeAdjacent;{ Отдельный расширяющийся цикл }

Procedure Var yes :Boolean );

i,j,k,m :Integer;

begin

{ Переназначение меток вершин }

{ их порядковыми номерами в списке смежности }

{ yes - признак правильной структуры списка смежности }

for i:=l to n do

for j:=l to Nbr[i] do begin yes:=FALSE; for m:=l to n do

if Adj [Fst[i]+j]=vtx[m] then begin yes:=TRUE; Adj[Fst[i]+j]:=m;

break;

end;

if not yes then expend;

{ Разместить петли в начале списка смежности } for i:=l to n do begin k:=l;

for j:=l to Nbr[i] do if Adj[Fst[i]+j]=i then begin

Adj[Fst[i]+j]:=Adj [Fst[i]+k];

Adj[Fst[i]+k]:=i;

k:=k+l; end;

end;

{ Степени вершин графа )

for i:=l to n do begin

Deg[i]:=0;

for to do begin

Deg[i]:=Deg[i]+l;

if then

end; end;

( Поиск начальной вершины ks цепи } k:=0; ks:=l;

for i:=l to n do if ( Deg[i] mod 2 ) > 0 then begin

k:=k+l; ks:=i; end;

if ( k<>2 ) and ( k<>0 ) then yes:-FALSE;

{ Граф не эйлеровый }

end;

Procedure v : .ntege .. var count : Integer );

{ Построение частной эйлеровой цепи г[ ] } Var

w :Integer;

i,j :Integer;

begin

count:=l; r[count]:=v;

repeat

w:=Adj[Fst[v]+1]; { Следующая вершина цепи > count:=count+l; r[count]:=w;

{ Удалить ребро (v,w) из списка смежности

для вершины v } Fst[v]:=Fst[v]+1; Nbr[v]:=Nbr[v]-1;

{ Если ребро (w,v) не петля, то удалить и его

из списка для вершины w } if vow then

for i:=l to Nbr[w] do if Adj [Fst [w]+i] =v then begin for j:=i+l to Nbr[w] do

Adj[Fst[w]+j-l] :=Adj [Fst[w]+j] ; Nbr[w]:=Nbr[w]-1; break; end; v: =w;

until Not( Mbrlvj>0 i; end;

Procedure { Построение эйлеровой цепи }

v,w :Integer;

i,j,kt ;Integer; count :Integer; yes :Boolean;

begin

v:=ks; kz:=l;

kt:=kz; z[kz]:=v;

Write (f,); {До объединения}

for i:=l to kz do Write(f,Vtx[z[i]]:3); WriteLn(f); repeat

Cycle(v,count) ;

Write(f, R= ) ;

for i:=l to count do

WriteLn(f) ;

for i:=l to count-1 do begin

z[kz+i]:=z[kt+i];

z[kt+i]:=r[i+1] ; end;

kz:=kz+count-l;

Write

for i:=l to kz do Write(f,Vtx[z[i]]:3); WriteLn(f); yes:=FALSE;

for i:=kz downto 1 do if Nbr[z[i]]>0 then begin v : = z [ i J ; kt:=i; yes:=TRUE; break; end; until Not yes; end;

Var (Main)

i, j :Integer; yes :Boolean; begin {Main}

Assign(f,Eiler.in);

Reset (f) ; {Фай.1 открыт для чтения}

{ Ввод списка смежности }

Read(f,n); (Количество строк в списке}

Fst[1]:-0; {Указате.щ начала первой строки списка}

for i:=l to n do begin

Read (f, Vtx [i] ) ; {Метка вершины}

Read(£,Nbr[i) ) ; {Количестве вершин в списке)

for j:=l to Nbr[i] do Read (f, Adj [ Fst [ i ]+j ].) ;

{Список смежных вершин} Fst[i+1]:=Fst[i]+Nbr[i];{Указатель начала следующей

строки в

end;

Close(f);

Assignff, Eiler.out);

открыт для

Init(yes) ;

if not yes then begin

WriteLn(f, Плохая структура смежности графа'); WriteLn(f, или граф не эйлеровый!); Close(f) ; exit;

end;

Eiler;

Write(f, 0=)

for i:=l to kz do Write(f,Vtx[z[i] ]:3) ; WriteLn(f); Close (f); end. (Main)

Рассмотрим пример расчета по программе алгоритма 6.6 поиска эйлеровой цепи в графе, изображенного на рис. 6.17.

Рис. 6.17. Пример расчета эйлеровой цепи графа

Для программы алгоритма 6.6 исходные данные структуры смежности графа на рис. 6.17 задаются в текстовом файле Eiler.in. Структура (правило) заполнения файла совпадает с той, которая описана в рассмотренном примере поиска в глубину при расчете по программе алгоритма 6.2.

Данные файла ЕИег.гпдля примера на рис. 6.17:

14 2 3

2 4 13

3 4 12

4 4 15

5 4 14

6 2 2 5

7 2 2 3

8 2 3 4

9 2 4 5

Результаты расчетов сохраняются в выходном файле Eiler.out со следующей структурой:

Z= 1

R = 1231451 Z = 1231451 R= 562738495

Z = 123145627384951 0 = 123145627384 951.

На каждом шаге показана строящаяся эйлерова цепь Z, которая расширяется выделенным R циклом. Результирующая эйлерова цепь графа отмечена признаком О в начале строки.

6.8. Остовные деревья

Определение. Остовиым деревом связного неориентированного графа (X, U, Ф) называется дерево = (X, U0, Ф) , являющееся подграфом графа Г и содержащее все его вершины (рис. 6.18).

Рис. 6.18. Связный граф и два остовных дерева