другое ребро. Если вершина у не пройдена, то заходим в нее и применяем процесс прохождения рекурсивно уже с вершиной у. Если все ребра, инцидентные вершине х, просмотрены:, то идем назад по ребру (s, х), по которому пришли в х, и продолжаем исследование ребер, ишгиденттньгх вершине s е X. Процесс заканчивается, когда попытаемся вернуться из вершины, с которой начали просмотр графа.

Поиск в глубину можно также осуществлять и на ориентированном графе. Если граф ориентированный, то, находясь в узлех, необходимо выбирать ребро (х, у), только выходящее из х. Исследовав все ребра, выходящие из у, возвращаемся в х даже тогда, когда в у входят другие ребра, еще не рассмотренные. Данная техника просмотра в глубину полезна в практических приложениях при определении различных свойств как ориентированных, так и неориентированных графов.

Метод поиска в глубину на простом неориентированном графе представлен в алгоритме 6.1. Рекурсивная процедура Depth(x, w) осуществляет поиск в глубину на графе Г= (X, U, Ф), содержащем е X, и строит для графа дерево Тпоиска, которое является ориентированным остовным деревом = (X, Т, Ф) (если исходный граф не связен, то Г0 будет лесом); w е является отцом х е Хв строящемся дереве, где х - исследуемая вершина. Граф задан структурой смежности Adj\x\ где Adj[x означает множество вершин, смежных с х е X. Элементы это ребра строящегося дерева поиска, а элементы В - это обратные ребра, которые не могут принадлежать так как они ведут назад в пройденные ранее вершины. Заметим, что обратное ребро должно идти от потомка к предку по дереву поиска. Чтобы отличить уже пройденные вершины от непройденных, вводится вектор Магк[х]м&-ток вершин, которые постепенно нумеруются от 1 до j по мере того, как попадаем в них. Сначала полагается Mark[х = 0 для всех х Хв знак того, что ни одна вершина не пройдена, и когда попадаем в вершинух первый раз, А/аг£[л:]получает ненулевое значение. Ребро (х, v) е Т, если метка вершины Mark[v = Если же Mark\v\t О, то условием того, что (х, v) & Сбудет обратным ребром, являются соотношения Markfv] < Магк[х и v w. Условие Mark[v] < Markfx] означает, что вершина v была пройдена раньше вершины х. Поэтому ребро (х, v) е В будет обратным, если оно не является ребром дерева Т, пройденным от отца w кх, т. е. v * w.

Сложность поиска в глубину. Поскольку. каждой вершины, которую проходим впервые, выполняется обращение к процедуре Depth ровно один раз, то всего обращений будет \Х\. При каждом обращении количество производимых действий пропорционально числу ребер, инцидентных рассматриваемой вершине. Поэтому сложность поиска составляет 0(\Х + \U\).

Алгоритм 6.1. Поиск в глубину на простом неориентированном графе

for v Xdo Mark[v = 0; count = 0; T=0;B=0; for v e Xdo ifMark[vY 0 then Depth(v, 0); procedure Depth(x, w); count= count + 1; Markfx] = count; for v e Adj[x] do begin ifMark[vlr 0 then

T= Tu{(x, v)}; { Включитьребро дерева } Depth(v, x); else ifMark[v]< Mark[x] and v * w then

В = В и {(x,v)}; { Включить обратное ребро }

end; end.

Программная реализация алгоритма представлена алгоритмом 6.2. Реализация близко соответствует основному алгоритму 6.1. Программа представлена тремя процедурами Init, Depth, Way-Depth, где WayDepth - основная программа поиска в глубину; Depth - рекурсивная процедура поиска, один к одному соответствующая аналогичной процедуре в алгоритме процедура контроля исходных данных и изменения меток вершин. Изменение нумерации меток вершин является существенным для алгоритма. Новые метки вершин - это натуральные числа от 1 до \Х\. Данная нумерация позволяет обращаться к элементам массивов, содержащих информацию о вершинах, по номерам соответствующих вершин. Такой прием позволяет очень близко подойти в программной реализацией структуры смежности Adj[x] к ее множественному описанию. В этом случае множественное описание выражения for v e Adj[ x do ... в программной реализации пред-

ставляется как/or / = 1 to Nbr[x] do v = Adj[Fst[x] + где МИ* - количество вершин в структуре смежности для вершины х X; Adj[x] - вектор, содержащий все вершины структуры смежности по строкам; Fst[x] + 1 - номер первой вершины структуре смежности для соответствующей вершины х е X, тогда Fst[x] + i - номер /-й вершины в структуре смежности для х в X.

Например, для следующей структуры смежности графа Adj[x\.

соответствующие массивы в программной реализации принимают вид

Исходные данные для расчета по программе алгоритма 6.2 представляются в текстовом файле со следующей структурой смежности Adj[x]:

в первой строке файла содержится количество строк в структуре смежности, которое равно числу вершин в графе;

далее для каждой вершины в отдельной строке указывается номер самой вершины, количество вершин, смежных с данной, и список этих вершин.

Рассмотрим пример расчета по программе алгоритма 6.2 обхода графа, представленного на рис. Сплошными линиями отмечены ребра, которые были пройдены во время обхода графа в глубину, пунктирными - обратные ребра.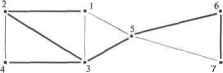

Рис. 6.13. Пример обхода графа в глубину

Исходные данные структуры смежности графа рис. 6.13 задаются в текстовом файле Depth, in:

1 3 2 3 5

2 3 13 4

3 4 1 2 4 5

4 2 2 3

5 4 1 3 6 7

6 2 5 7

7 2 5 6

Результаты расчетов сохраняются в выходном файле Depth.out со следующей структурой:

1233435567 X,

2314251675 Л' 1101010110 TvB

Каждая колонка таблицы выходного файла соответствует ребру *Л->() прохода графа, где последнее значение является признаком 1 или 0, что отвечает при проходе либо основному ребру, либо обратному.

Алгоритм 6.2. Программа поиска в глубину на простом неориентированном графе

Program {Проход графа в глубину}

uses CRT,DOS;

Const

nVertex--100; ( Максимальное количество вершин ! nftdjacent=1000; {Максимальная длина списка смежности! Туре

TypeVertex=array[l..nVertex] of Integer; TypeAdjacent=array[1..nAdjacent] of Integer;

в глубину }

В :TypeVertex; { Признаки основных и обратных ребер

прохода в глубину }

Procedure Var yes :Boolean ) ;

{ Переназначение меток вершин } { их порядковыми номерами в списке смежности } { yes - признак правильной структуры списка смежности } Var

i, j,m :Integer;

begin

for i:=l to n do

for j:=l to Nbrfi] do begin yes:=FALSE; for to n do

if Adj[Fst[i]+j]=Vtx[m] then begin yes:=TRUE; Adj[Fst[i]+j]:=m; break; end;

if not yes then exit; end;

end;

Procedure var count : Integer) ;

i,v :Integer; begin

count:=count+l; Mark[x]:=count;

for i:=l to do begin

v:=Adj[Fst[x]+i];

if then begin

nT:=nT+2; T[nT-l]:=x; T[nT]:=v; B[nT div 2] :=1; {Прямое ребро) Depth(v,x,count); end

else if (Mark[v]<Mark[x] ) and (vou) then begin {Обратное ребро)

nT:=nT+2; T[nT-l]:=x; T[nT]:=v;

B[nT div 2]:-0; {Обратное ребро} end; end;

end;

Procedure {Проход: в глубину)

v,count :Integer;

begin

пТ:=0; {T - пустое дерево) count:=0;

for v:=l to n do Marklv):=0;

for v:=l to n do if Mark[v]=0 then Depth(v,0,count); end;

Var {Main)

i,j :Integer; yes :Boolean; begin {Main)

Assign(f,Depth.in);

Reset(f);{Файл открыт для чтения} ( Ввод списка смежности }

Read(f,n); {Количество строк в списке}

Fst[l]:=0; {Указатель начала первой строки списка}

for i:=l to n do begin

Read (f,Vtx[i]); {Метка вершины) Read(f,Nbr[i)) ; {Количестве вершин в списке} for j:=l to Nbr[i] do Read (f, Adj [Fst [ i ] + j ] ) ; ICm:coi. смежных вершин}

следующей строки в списке}

end;

Close

Assign(f,Depth.out);

открыт для

Init(yes);

if not yes then begin

WriteLn(f,Плохая структура смежности графа!);

Close (f) ;

exit ; end;

WayDepth;

for i:=l to nT div 2 do Write(f,Vtx[T[2*i-l]): 3); Writeln(f);

for i:=l to nT div 2 do

Writeln(f);

for i:=l to nT div 2 do

Close(f); end. {Main)

6.4. Отношение эквивалентности

Бинарное отношение ~, определенное на множестве S, называется отношением эквивалентности, если оно удовлетворяет свойствам рефлексивности, симметричности и транзитивности:

1. vs, е S s{~ sv

2. vs s2 е S ~ s2 -> s2 ~

3. Щ, s2, 53 e S Щ ~ s2 л a ~ s3 - Sj ~ sy

Все элементы из множества S, эквивалентные данному элементу образуют множество которое называется классом эквивалентности. Два различных класса эквивалентности не могут иметь какого-либо общего элемента, в противном случае такие классы совпадают, что следует из свойств 1-3. Таким образом, определенное на множестве S отношение эквивалентности выполняет разложение его на непересекающиеся классы эквивалентности, т.е. S - {JSj где S,r\ S, = 0, i - /. I

Пример. Пусть множество треугольников. Определим на S бинарное ~ отношение. Будем считать, что для треугольников S выполняется отношение Да ~ если они подобные. Ясно, данное отношение является отношением эквивалентности, так как свойства 1-3 выполняются для подобных треугольников. Введенное отношение разбивает множество треугольников на классы эквивалентности подобных треугольников.

Пример. Пусть множество векторов. Определим

на S бинарное ~ отношение. Будем полагать, что для e S выполняется отношение а ~ если они Данное отношение является отношением эквивалентности, так как свойства 13 выполняются для колинеарных векторов. Множество векторов под действием введенного отношения разбивается на классы эквивалентности колинеарных векторов.

Пример. Пусть Определим на бинарное ~ от-

ношение. Будем полагать, что дляр, q e Sвыполняется отношение р ~ q, если они имеют одинаковые остатки от деления на целое положительное число т. Данное отношение является отношением эквивалентности. Множество £под действием введенного отношения разбивается на классы эквивалентности чисел с одинаковыми остатками от деления на т.

Пример. Пусть множество треугольников. Определим на S бинарное ~ отношение. Будем считать, что для треугольников Да, Ab е 5выполняется отношение Да ~ Ab, если их площади равны. Данное отношение является отношением эквивалентности.

6.5. Связные компоненты

Пусть псевдограф Г= (X, U, Ф) является неориентированным. Две вершины хь х2 е X называются связанными, если существует маршрут изХу вх2. Определим на множестве вершин ЛГбинарное ~ отношение. Для xlt х2& X отношение ~ будет выполняться, т.е. Ху ~ х2, если эти вершины связанные. Введенное отношение является отношением эквивалентности. Действительно, если вершина Ху связана с х2, а вершина х2 связана с х3, то очевидно, что вершинах! связана с х3. Следовательно, существует такое разложение множества вершин

X=[JXt

на попарно непересекающиеся подмножества, что все вершины в каждом Д связаны, а вершины из различных Дне связаны. Тогда можно записать разложение

r=\jruc uit0)

графа Г= (X, U, Ф) на непересекающиеся связные подграфы Г= (Xit Uj, Ф). Вследствие попарного непересечения подграфов, разложение называется прямым, а сами подграфы называются компонентами связности графа Г. Таким образом, справедливо следующее утверждение.

Утверждение 6.5.1. Каждый неориентированный граф распадается единственным образом в прямую сумму своих компонент связности.

Количество компонент связности находится в определенном отношении с основными параметрами графа - числом его вершин и ребер.

- Утверждение 65.2. ПустьГ= (X, U, Ф) является простым графом с п вершинами и £ компонентами связности. Число ребер в таком графе не может превосходить величины Cf k+l =

= (n-k + l)(n-k)/2.

Доказательство. Рассмотрим прямое разложение

к

Г= ]Г(Хри1гФ) исходного графа на компоненты связности.

Если положить, что число вершин в компоненте связности рав-

к ,

но л„ то число ребер в таком графе не превосходит Данная

величина достигается в том случае, когда каждая из компонент связности является полным подграфом. Допустим, что среди компонент связности Г(Хп Ur Ф) найдутся хотя бы две, которые имеют более одной вершины, например щгщ > 1. Перенесем одну вершину из /\ в Г2. Легко видеть, что это увеличивает число ребер в модифицируемом полном графе, с к компонентами связности. Отсюда следует, что максимальное число ребер должен иметь граф, состоящий из к - 1 изолированной вершины и одного полного подграфа с п - к + 1 вершинами.

Следствие. Граф с п вершинами и числом ребер, большим чем связен.

6.6. Выделение компонент связности

Рассмотрим алгоритм нахождения числа компонент связности, а также выделения этих компонент на неориентированном графе. Подобным образом решается задача и для ориентированного графа. В основу рассматриваемого алгоритма 6.3 выделения компонент связности положена описанная ранее техника поиска в глубину на графе Г(Х, U, Ф). Структура алгоритма 6.3 является модификацией в сторону упрощения основного алгоритма 6.1 поиска в глубину. Работа алгоритма 6.3 направлена на формирование вектора меток вершин х е X графа. Элементу Магк[х] присваивается общий номер той компоненты, которой принадлежит вершинах е X. Сложность алгоритма 6.3, как и алгоритма 6.1, составляет + \U\).

Алгоритм 6.3. Выделение связных компонент неориентированного графа

for v е Xdo Mark[v]= 0; {Начальнаяустановка} count = 0; {Счетчик числа компонент) for v & Xdo ifMark[vb 0 then begin count = count + 1; Component, count); end;

Procedure Component(x, count): Mark[x] = count;

for v е Adj[x] do if Mark{vY 0 then Component, count);

end;

Программная реализация выделения компонент связности представлена в алгоритме 6.4, который близко соотносится с соответствующим множественным описанием алгоритма 6.3. Рассмотрим пример расчета по программе алгоритма 6.4 выделения компонент связности графа, представленного на рис. 6.14.

Рис. 6.14. Пример выделения компонент связности графа

Для программы алгоритма 6.4 исходные данные структуры смежности графа на рис. задаются в текстовом файле

Connect.in. Структура (правило) заполнения файла одинакова с той, которая описана в рассмотренном примере поиска в глубину при расчете по программе алгоритма 6.2.

Данные файла Connect.in для примера на рис. 6.14:

Результаты расчетов сохраняются в выходном файле Соп-

nect.out со следующей структурой:

1 2 9 8 12 14 з 4 7 15 21 - номера вершин графа;

номера компонент связности.