s + 1. Алгоритм не содержит вложенных циклов, а значит, сложность его линейная 0(п).

Допускаются одинаковые значения среди я

Реализация метода представлена в алгоритме 5.10. Наличие одинаковых элементов среди например, = при

упаковке Ьа =й,- nba = ; ведет к потере данных в исходном множестве flj, а-у,--, ап. Ситуация, когда одновременно несколько элементов претендуют на одно место, называется коллизией. Такие элементы необходимо переразмещать на свободные места, сохраняя свойства сортировки с вычисляемыми адресами. С этой целью на основании величин рассчитывается вектор индексов сортированной упаковки данных в массиве by b,--, bH. В алгоритме 5.9 роль индексов упаковки могли выполнять непосредственно сами значения элементов

так как они были различные. В данном случае значения таким образом, что одинаковые по величине элементы из оказываются смежными при их упаковке в массиве by Ь2,..., Ьп. Вектор сп cr+ у..., cs используется для подсчета количества элементов каждого значения среди flj, щ ,., а„ и формирования индексов упаковки dr, drH,..., ds.

Алгоритм 5.10. Сортировка с вычисляемыми адресами для произвольныхви 02,..., ап

{Поискmin и max значений среди аь а2,..., а„ } r s а.:

for i-2 ton do begin ifr>Oj then r= flj else ifs < a> then s = щ end;

{Расчет количества элементов каждого значения а, }

for i = rto s do С; = 0; fori=\ tondocai =ca: +1;

{Расчет индексов упаковки dn dy..., ds } dr=\;

fori = r+ltos do dj = flf,. ! +

{Сортированнщпаковкаэлементовщ, a2,..., a в by b2,..., bn > for i = 1 to n do begin k = a,;

dk = dk + 1; end.

Резулъшрующий сортированный вектор исходных данных щ, о2,..., ап располагается в массиве bi<b2< ... < Ьп. Алгоритм не содержит вложенных циклов, а значит сложность его линейная О(п).

Сортировка с вычисляемыми адресами является очень быстрым методом, но она может быть крайне неэффективной при больших значенияхs - /-сточки зрения использования оперативной памяти, необходимой для хранения временных массивов данных сп Cr+j,..., cs и dr, 4+lr...s ds.

Глава 6

ВВеГгНоиреитВмЫеонраигЭраГфааффоВ-

.S-l ножество самых разнообразных задач естественно формулируется в терминах точек и связей между ними, т.е. в терминах графов. Так, например, могут быть сформулированы задачи составления расписания, анализа сетей в электротехнике, анализа цепей Маркова в теории вероятностей, в программировании, в проектировании электронных схем, в экономике, в социологии и т.д. Поэтому эффективные алгоритмы решения задач теории графов имеют большое практическое значение.

6.1. Основные понятия и определения

Определение. Конечным графом называется тройка Г= (X, U, Ф), где X- конечное множество вершин; U- конечное множество ребер (дуг); Ф - отношение инцидентности; Xc\U= 0. Отношение инцидентности Ф является трехместным отношением Ф(х, и, у), где х,уеХ, и е U, которое может

либо выполняться (быть истинным), либо не выполняться (быть ложным) и удовлетворяет свойствам:

1) Уи е U Зх,у еХ Ф(х, и, у) - ребро всегда соединяет пару вершин.

2) (Ф(х, и, у) л Ф(х', и, у)) => ((х=х'лу = у) v (х=у'лу = х)) -ребро и соответствует не более чем одной паре вершин х, у.

Графическое представление графов.

Элементы графов

1. х е X - вершина.

2. Ф(х, и, у) л -, Ф(у, и, х) -ориентированное ребро, дуга.

3. Щх, и, у) л Ф{у, и, х) -неориентированное ребро.

4. Ф(х, и, х) - петля.

Геометрические элементы

1. - точка в пространстве. 2.x--у- направленный отрезок.

3.x---у - отрезок.

4. Х& - замкнутый отрезок.

Рис. Графы с тремя вершинами и двумя ребрами

Определение. Гх (Хь U{, Фу) иГ2 ={Х2, U2, Ф2) называются изоморфными /2) если существуют два взаимно однозначных соответствия : А'( ->Aj и : Vy U2, сохраняющие отношение инцидентности: Ф2(ц>(ху),ц1(и]),ц>(уу)) = Фу(х],иу,ух). Из определения следует, что изоморфные графы можно одинаково изображать графически и отличаться они будут только метками вершин (рис. 6.2).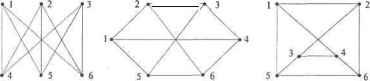

Рис. 6.2. Три изоморфных графа

Определение. Граф называется ориентированным (орграф), если каждое его ребро ориентировано: УхуеХУи<~ U Ф(х, и, у) => Ф(у, и, х). Иногда удобно преобразовать неориентированный граф в ориентированный - заменой каждого неориентированного ребра парой ориентированных ребер с противоположной ориентацией.

Определение. Подграфом графа Г= (X, U, Ф) называется такой граф Г= (X, и\ Ф), что XczX, UczU. Обозначают Г'с Г.

Определение. Граф называется псевдографом, если в нем допускаются петли и кратные ребра, т. е. две вершины могут быть соединены более чем одним ребром. Псевдограф без петель называется мулътиграфом (рис. 6.3).

Рис. 6.3. Псевдограф (слева) и мультиграф (справа)

Определение. Неориентированный граф называется простым, если он не имеет петель и любая пара вершин соединена не более чем одним ребром.

Определение. Простой граф называется полным, если каждая пара вершин соединена ребром. Такой граф с п вершинами содержит С„2 ребер (рис. 6.4).

Рис. 6.4. Полные неориентированные графы

Определение. Дополнением простого графа Г называется граф имеющий те же вершины, а его ребра являются дополнением Г до полного графа (рис. 6.5).

Рис. 6.5. Исходный граф Г и дополнительный Г

Определение. Граф называется плоским {планарным) если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами.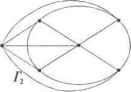

неплоский

Рис. 6.6. Граф Г, - плоский, а граф Г2

Определение. Если верши*ш х у соединены ребром и, то говорят, что вершины х, у смежные, а ребро и инцидентно вершинам х и у. Два ребра называются смежными, если они имеют общую вершину.

Определение. Степенью вершины графа называется количество ребер, инцидентных данной вершине. Вершина графа, имеющая степень 0, называется изолированной, а если степень ее равна 1, то такая вершина называется висячей.

Определение. Граф называется помеченным (или перенумерованным), если его вершины отличаются друг от друга какими-либо пометками (рис. 6.7).

Рис. 6.7. Граф Г, - помеченный, а граф Г2 - непомеченный

Определение. Путь (маршрут) на графе (X, U, Ф) определяется последовательностью вершин и ребер xlulx2u2xJ...xnuflxn+b где Xj е X, ще U. Ребро щ соединяет вершину х, с вершиной xj+ т.е. выполняется отношение инцидентности Ф{х„ u xh Y).

Маршрут называется цепью, если все его ребра различные.

Маршрут называется замкнутым, если =х Л-

Замкнутая цепь называется циклом.

Цепь называется простой, если не содержит одинаковых вершин.

Простая замкнутая цепь называется простым циклом.

Гамилыпоновой цепью называется простая цепь, содержащая все вершины графа.

Гамильтонавым циклом называется простой цикл, содержащий все вершины графа.

Определение. Граф Г= (X, U, Ф) называется связным, если для всех х, у е Хсуществует путь из вершины в вершину у (вершины хиу связаны маршрутом). Связный ориентированный граф называется сильно связным. Орграф называется слабо связным, если соответствующий ему неориентированный граф (игнорируется ориентация ребер) связный (рис. 6.8).

Рис. 6.8. Г, - слабо связный, Г2 - сильно связный

Определение. Связный неориентированный ациклический граф называется деревом, множество деревьев называется лесом.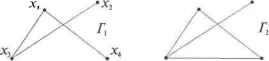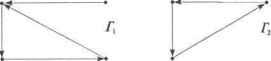

Рис. 6.9. - дерево, - не дерево

Большинство задач на графах касается определения компонент связности, поиска маршрутов, расстояний и т.п. Далее будут рассмотрены решения подобных вопросов. Однако при решении реальных задач соответствующие им графы весьма велики, и анализ возможен лишь с привлечением современной вычислительной техники. Поэтому конечной целью рассмотрения каждой из задач будет являться описание и реализация практического алгоритма решения данной задачи на ЭВМ.

6.2. Представления графов

Наиболее известный и популярный способ представления графов состоит в геометрическом изображении точек (вершин) и линий (ребер) на бумаге. При численном решении задач на вычислительных машинах должен быть представлен дискретным

способом. Существует довольно много способов такого рода

представления графов. Однако простота использования представления графа, как и эффективность алгоритма, в основе которого он лежит, в полной мере зависит от конкретного выбора этого представления. Одно из направлений теории графов связано с

их матричным представлением. Существуют различные виды

матриц, ассоциированные с графами. Эти алгебраические формы

используются для решения многих задач теории графов. Ниже рассматриваются две такие матричные формы и несколько нестандартных представлений, которые наиболее широко используются в алгоритмах на графах.

6.2.1. Матрица смежности графа

Определение. Матрицей смежности ориентированного помеченного графа с вершинами называется матрица А= [й,;], i,j=l, 2,..., п, в которой

(1, если существует ребро (xXj), ,J ) 0, если вершины ,Xj не связаны ребром (х, ,х,),

Матрица смежности однозначно определяет структуру графа. Примеры орграфа и его матрицы: смежности приведены соответственно на рис. 6.10 и рис. 6.11. Отметим, что петля в матрице смежности может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы: быть больше 1, но это не принято, обычно же представляют каждый элемент матрицы: одним двоичным разрядом.

Рис. 6.10. Ориентированный граф

Рис. 6.11. Матрица смежности ориентированного графа рис. 6.10

6.2.2. Матрица инцидентности графа

Определение. Матрицей инцидентности для неориентированного графа с п вершинами и т ребрами называется матрица B = [by], i = 1, 2,...,n,j = 1, 2,..., т, строки которой соответствуют вершинам, а столбцы: - ребрам. Элементы

если вершина не инцидентна ребру

Определение. Матрицей инцидентности для ориентированного графа с п вершинами и т ребрами называется матрица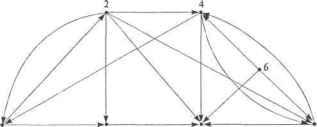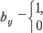

если вершина инцидентна ребру

1,2,..,/?,/= 1, т, строки которой соответствуют вершинам, а столбцы - ребрам. Элементы

если ребро выходит из вершины -1, если ребро Uj входит в вершинух О, если вершина не инцидентна ребру и;.

Матрица инцидентности однозначно определяет структуру графа. На рис. 6.12 представлена такая матрица для орграфа на рис. 6.10.

II 1 1 11 11 4 4 4 6 6 6 7.7 231 34575 15745745

l[+l +1 -1 00000 -1 000000 0

2 -1 0 +1 +1 +1 +1 +1 0 0 0 0 ОО ООО

3 0 -1 0 -1 000 +1 000 00000 Я = 4 О О О 0 -1 0 0 0 +1 +1 +1 -1 0 0 -1 О

5 О 0 0 0 0 -1 0 -1 0 -1 0 0 -1 0 0 -1 00000000 0 0 0 +1 +1 +1 0 0 \ О 0 0 0 0 0 -1 0 0 0 -1 0 0 -1 +1 +1

Рис. 6.12. Матрица инцидентности ориентированного графа

6.2.3. Матрица весов графа

Определение. Граф называется взвешенным, если каждому его ребру сопоставлено число. Простой взвешенный граф может быть представлен своей матрицей весов W= [w, где Wy- вес ребра, соединяющего вершины 1, п. Веса несуществующих ребер полагают равными или 0 в зависимости от приложений. Заметим, что матрица весов является простым обобщением матрицы смежности.

6.2.4. Список ребер графа

При описании графа списком его ребер каждое ребро представляется парой инцидентных ему вершин. Это представление можно реализовать двумя массивами г = (гъ г2,..., гт) и t= (rl512,..., tm), где т - количество ребер в графе. Каждый элемент в массиве есть метка вершины, а /-е ребро графа выходит из вершины rt и входит в вершину г,. Например, соответствующие массивы представления графа на рис. 6.10 будут иметь вид:

r= (1, 1, 2, 2, 2, 2, 2, 3, 4, 4, 4, 6, 6, 6, 7, 7),

Г=(2, 3, 1, 3,4, 5, 7, 5, 1, 5,7,4, 5, 7,4, 5).

Интересно, что данное представление позволяет легкоописать петли и кратные ребра.

6.2.5. Структура смежности графа

Ориентированный или неориентированный граф может быть однозначно представлен структурой смежности своих вершин. Структура смежности состоит из списков Adj[x вершин графа, смежных с вершиной х. Списки Adj[x] составляются для каждой вершины графа. В качестве примера опишем структуру смежности графа, представленного на рис. 6.10.

Структуры смежности могут быть удобно реализованы массивом из п (число вершин в графе) линейно связанных списков. Каждый список содержит вершины, смежные с вершиной, для которой составляется список. Хранение же списков смежности на сцепленной памяти желательно в алгоритмах, в основе которых лежат операции добавления и удаления вершин из списков. Следует отметить, что во многих задачах на графах выбор представления является решающим для эффективности алгоритмов.

6.3. Метод поиска в глубину

Один из наиболее естественных способов систематического исследования всех вершин графа исходит из процедуры прохождения графа методом поиска с возвращением, который исследует граф в глубину (см. п.4.1). На неориентированном графе Г - (X, U, Ф) поиск в глубину осуществляется следующим образом. Когда посещаем вершину X, то далее идем по одному из ребер (х, у), инцидентному вершине у е X. Если вершина у уже

пройдена (посещалась ранее), то возвращаемся в х и выбираем