- функция Муни - Ривлина при KEYOPT(2) = 0;

- EX при KEYOPT(2) = 1.

Нагрузки, прикладываемые к поверхности элемента:

- давление - на грани (ребре) 1 (J-1), на грани (ребре) 2 (K-J), на грани (ребре) 3 (L-K), на грани (ребре) 4 (I-L).

Объемные нагрузки:

- температуры - T(I), T(J), Т(К), T(L), Т(М), T(N), Т(О), Т(Р), в зависимости от числа узлов.

Специальные возможности:

- большие перемещения;

- большие деформации.

KEYOPT(l) - признак формулировки элемента:

- 0 - элемент I порядка с четырьмя узлами;

- 1 - элемент II порядка с восемью узлами.

KEYOPT(2) - признак функции энергии упругих деформаций:

- 0 - почти несжимаемый материал Муни - Ривлина (Mooney - Rivlin), для указания констант применяется команда TBDATA;

- 1 - сжимаемый материал Блатца - Ко (Blatz-Ko).

KEYOPT(3) - признак напряженно-деформированного состояния:

- 0, 2 - плоское деформированное состояние;

- 1 - осесимметричное НДС.

KEYOPT(4) - признак системы координат элемента:

- 0 - система координат элемента параллельна глобальной системе координат;

- 1 - система координат элемента основана на ребре I-J недеформированно-го элемента.

KEYOPT(5) - признак вывода внешних напряжений:

- 0 - вывод базовых объектов;

- 1 - вывод деформаций в элементе;

- 2 - вывод напряжений в точках интегрирования;

- 3 - вывод деформаций в точках интегрирования;

- 4 - вывод узловых напряжений;

- 9 - полный вывод данных (включая все опции).

KEYOPT(6) - признак интегрирования:

- 0 - полное интегрирование энергии деформаций;

- 1 - полное интегрирование касательных членов и редуцированное интегрирование объемных членов энергии деформаций.

Расчетные данные элемента

Выходная расчетная информация, связанная с элементом, разделена на два вида:

- дополнительные элементные объекты, перечисленные в табл. 2.45.

Признак KEYOPT(5) обеспечивает различные опции вывода данных. Направления напряжений в элементе параллельны системе координат элемента.

2.10.46. HYPER86 - двухмерный (2D) гиперупругий элемент объемного НДС

Описание элемента

Элемент HYPER84 используется для моделирования в трехмерной (3D) постановке объемных конструкций, работающих в условиях гиперупругости. Данный элемент применим к подобным резине материалам, подвергаемым произвольно большим перемещениям и деформациям. Элемент пригоден для моделирования сжимаемых или почти несжимаемых материалов. Формулировка гиперупругости является нелинейной и требует применения итерационного расчета. Для обновления геометрии на каждом промежуточном шаге опция больших перемещений должна являться активной (команда NLGEOM).

Имеющиеся опции позволяют указывать тин функции плотности энергии деформаций, расположение точек вывода данных в элементе и редуцированного интегрирования. Аналогичным элементом (без применения гиперупругости) является SOLID45. Двухмерной (2D) версией данного гиперунругого элемента является HYPER84.

Исходные данные элемента

Геометрия, расположение узлов и система координат элемента показаны на рис. 2.46. Элемент определяется восемью узлами и свойствами изотропного материала. Исходные данные элемента включают функцию'энергии деформаций (KEYOPT(2)) и константы, определяющие функцию энергии деформаций Муни - Ривлина (Mooney - Rivlin).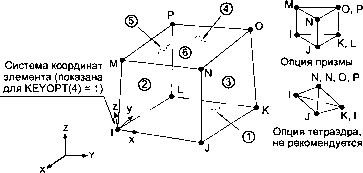

Рис. 2.46. Геометрия элемента HYPER86

Признак KEYOPT(2) позволяет указывать функцию энергии деформаций. Функция Муни - Ривлина (Mooney - Rivlin) применима для широкого диапазона почти несжимаемых материалов типа резины й ей подобных. Она характеризуется коэффициентом Пуассона и константами а!0 и а01 (указываемыми командами TBDATA или *MOONEY), которые, в свою очередь, могут зависеть от температуры. Функция Блатца - Ко (Blatz-Ko) может применяться для материалов типа сжимаемого пеноподобного пенополиуретана. Она является функцией начального модуля сдвига материала (вычисленного на основе модуля Юнга ЕХ и коэффициента Пуассона (PRXY или NUXY)).

Признак KEYOPT(5) обеспечивает различные опции вывода информации. Признак KEYOPT(6) обеспечивает опцию выбора схемы редуцированного интегрирования функции энергии деформаций для преодоления объемного запирания (применяется только для модели материала Муни - Ривлина (Mooney -Rivlin)).

Список исходных данных элемента

Узлы-LJ, К, L, M,N, О, Р.

Степени свободы - UX, UY, UZ. Геометрические характеристики - нет. Свойства материала:

- PRXY (или NUXY), DENS, DAMP;

- функция Муни - Ривлина при KEYOPT(2) = 0;

- EX при KEYOPT(2) = 1.

Нагрузки, прикладываемые к поверхности элемента:

- давление - на грани 1 (J-I-L-K), на грани 2 (I-J-N-M), на грани 3 (J-K-0-N), на грани 4 (K-L-P-О), на грани 5 (L-I-M-P), на грани 6 (M-N-О-Р).

Объемные нагрузки:

Специальные возможности:

- большие перемещения;

- большие деформации.

KEYOPT(2) - признак функции энергии упругих деформаций:

- О - почти несжимаемый материал Муни - Ривлина (Mooney - Rivlin), для указания констант применяется команда TBDATA;

- 1 - сжимаемый материал Блатца - Ко (Blatz-Ko).

KEYOPT(4) - признак системы координат элемента:

- О - система координат элемента параллельна глобальной системе координат,

- 1 - система координат элемента основана на ребре I-J недеформированно-го элемента.

KEYOPT(5) - признак вывода внешних напряжений:

- О - вывод базовых объектов;

- 1 - вывод деформаций в элементе;

- 2 - вывод напряжений в точках интегрирования;

- 3 - вывод деформаций в точках интегрирования;

- 4 - вывод узловых напряжений;

- 9 - полный вывод данных (включая все опции). KEYOPT(6) - признак интегрирования:

- О - полное интегрирование энергии деформаций;

- 1 - полное интегрирование касательных членов и редуцированное интегрирование объемных членов энергии деформаций.

Расчетные данные элемента

Выходная расчетная информация, связанная с элементом, разделена на два вида:

- узловые объекты, такие как узловые перемещения, включены в полное узловое решение;

- дополнительные элементные объекты, перечисленные в табл. 2.46. Направления напряжений в элементе параллельны системе координат эле-

Таблица 2.46. Описание расчетных данных элемента HYPER86

Определение

NODES

VOLU

XC.YC, ZC PRES

TEMP

S:X,Y,Z,XY,YZ,XZ S: 1, 2, 3 S:INT

Номер элемента

Номера узлов элемента - I, j, К, L, (М, N, о, Р) Номер материала, используемого для элемента Объем элемента

Координаты точки, в которой вычисляются результаты

Давление Р1 в узлах j, I, L, К; Р2 в I, j, N, М; Р3 в j, К, О, N; Р4 в К, L, Р, О; Р5 в L, I, М, P;P6bM,N,QP

Температуры - T(l), T(J), T(K), T(L), T(M), T(N), Т(О), Т(Р)

Напряжения

Главные напряжения

Интенсивность напряжений (эквивалентное напряжение по Трескау и Сен-Венану)

Таблица 2.46. Описание расчетных данных элемента HYPER86 (продолжение)

Объект Определение

S:EQV Эквивалентное напряжение (по фон Мизесу)

EPELX, Y, Z, XY YZ, XZ Упругие деформации

EPEL: EQV Эквивалентная упругая деформация

ЕРТН:Х, X Z, XY, YZ, XZ Средние температурные деформации

UNEXTN Единичное удлинение (Х,Х Z)

liOTANG Изменение углов (XY; YZ, XZ)

2.10.47. VISC088 - двухмерный (2D) вязкоупругий элемент объемного НДС с восемью узлами

Описание элемента

Элемент VISC088 является квадратичным (II порядка) изопараметрическим элементом. Элемент определяется восемью узлами, имеющими по две степени свободы в каждом узле: перемещения в направлении осей X и Y узловой системы координат. Элемент может,использоваться для моделирования плоского напряженного состояния или в виде осесимметричного элемента. Элемент имеет различные опции вывода данных.

Исходные данные элемента

Геометрия, расположение узлов и система координат элемента показаны на рис. 2.47. Элемент треугольной формы может быть получен путем указания равных значений координат для узлов К, L и О. Элемент VISC088 использует модель вязко-упругого материала, указываемую командами ТВ и TBDATA. Таблица констант вызывается командой ТВ с аргументом Lab = EVISC. При помощи команды TBDATA можно указать до 95 констант.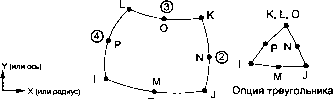

Рис. 2.47. Геометрия элемента VISC088

Список исходных данных элемента

Узлы-LJ, К, L, M,N, О, Р. Степени свободы - UX, UY. Геометрические характеристики - нет.

Свойства материала - DAMP, DENS и константы вязкоупругого материала. Нагрузки, прикладываемые к поверхности элемента:

- давление - на грани (ребре) 1 (J-1), на грани (ребре) 2 (K-J), на грани (ребре) 3 (L-K), на грани (ребре) 4 (I-L).

Объемные нагрузки:

- температуры - T(I), ТО), Т(К), T(L), Т(М), T(N), Т(О), Т(Р). Специальные возможности:

- вязкоупругость;

- увеличение жесткости при наличии нагрузок;

- адаптивный спуск

KEYOPT(3) - признак напряженно-деформированного состояния:

- О, 2 - плоское деформированное состояние (деформация в направлении оси Z равна 0);

- 1 - осесимметричное НДС.

KEYOPT(5) - признак вывода внешних напряжений:

- 0 - вывод базовых объектов;

- 1 - дополнительный вывод базовой информации во всех точках интегрирования;

- 2 - вывод узловых напряжений. Расчетные данные элемента

Выходная расчетная информация, связанная с элементом, разделена на два вида:

- узловые объекты, такие как узловые перемещения, включены в полное узловое решение;

- дополнительные элементные объекты, перечисленные в табл. 2.47.

Направления напряжений в элементе параллельны осям глобальной декартовой системы координат.

Таблица 2.47. Описание расчетных данных элемента VISC088

Объект Определение

EL Номер элемента

NODES Номера узлов элемента - I, J, К, L, (М, N, О, Р)

МАТ Номер материала, используемого для элемента

VOLU Объем элемента

XC, YC Координаты точки, в которой вычисляются результаты

PRES Давление Р1 в узлах J, I; Р2 в К, J; РЗ в L, К; Р4 в I, L

TEMP Температуры - T(l), T(J), T(K), T(L), Т(М), T(N), Т(О), Т(Р)

S:X, XZ, XV Напряжения

S: 1,2,3 Главные напряжения

S: INT Интенсивность напряжений (эквивалентное напряжение по Трескау и Сен-Венану)

S: EQV Эквивалентное напряжение (по фон Мизесу)

EPEL:X, X Z, XY, YZ, XZ Упругие деформации

EPEL: EQV Эквивалентная упругая деформация

ЕРТН:Х, X Z, ХУ, YZ, XZ Средние температурные деформации

EPTH:EQV Эквивалентная температурная деформация

2.10.48. VISC089 - трехмерный (3D) вязкоупругий элемент с двадцатью узлами

Описание элемента

Элемент VISC088 является квадратичным (II порядка) изопараметрическим элементом. Элемент определяется двадцатью узлами, имеющими по три степени свободы в каждом узле: перемещения в направлении осей X, Y и Z узловой системы координат. Элемент имеет различные опции вывода данных.

Исходные данные элемента

Геометрия, расположение узлов и система координат элемента показаны на рис. 2.48. Элемент призматической формы может быть получен указанием идентичных координат для узлов К, L и S; узлов А и В и узлов О, Р и W. Элемент в форме тетраэдра и пирамиды также может быть создан, как показано на рис. 2.48. Элемент VISC089 использует модель вязкоупругого материала, указываемую командами ТВ и TBDATA. Таблица констант вызывается командой ТВ с аргументом Lab = = EVISC. При помощи команды TBDATA можно указать до 95 констант.

Признак KEYOPT(5) обеспечивает различные опции вывода расчетных данных в элементе.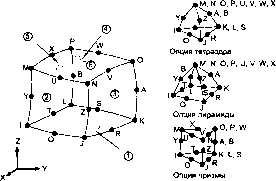

Список исходных данных элемента

Узлы - I, J, К, L, М, N, О, Р, Q, R, S, Т, U, V, W, X, Y, Z, А В. Степени свободы - UX, UY, UZ. Геометрические характеристики - нет.

Свойства материала - DAMP, DENS и константы вязкоупругого материала. Нагрузки, прикладываемые к поверхности элемента:

- давление - 1 - на грани JILK, 2 - на грани IJNM, 3 - на грани JKON, 4 - на грани KLPO, 5 - на грани LIMP, 6 - на грани MNOP.

Объемные нагрузки:

- температуры - T(I), TYJ),..., T(Z), Т(А), Т(В). Специальные возможности:

- вязкоупругость;

- увеличение жесткости при наличии нагрузок;

- адаптивный спуск.

KEYOPT(5) - признак вывода внешних напряжений:

- О - вывод базовых объектов;

- 1 - дополнительный вывод базовой информации во всех точках интегрирования;

- 2 - вывод узловых напряжений. Расчетные данные элемента

Выходная расчетная информация, связанная с элементом, разделена на два вида:

- узловые объекты, такие как узловые перемещения, включены в полное узловое решение;

- дополнительные элементные объекты, перечисленные в табл. 2.48.

Таблица 2.48. Описание расчетных данных элемента VISC089

Таблица 2.48. Описание расчетных данных элемента VISC089 (продолжение)

2.10.49. SHELL91 - нелинейная многослойная оболочка

Описание элемента

Элемент SHELL91 может применяться для расчета НДС многослойных оболочек или задач с большим количеством тонких слоев. При использовании элемент SHELL99 обычно эффективнее элемента SHELL91. При отключенной опции трехслойной конструкции можно использовать до 100 слоев. Элемент SHELL99 позволяет большее число слоев, но без нелинейных свойств материалов. Элементом многослойного объемного тела является SOLID46.

Элемент имеет шесть степеней свободы в каждом узле: перемещения в направлении осей X, Y и Z узловой системы координат и повороты вокруг осей X, Y и Z узловой системы координат.

Исходные данные элемента

Геометрия, расположение узлов и координатная система элемента показаны на рис. 2.49. Элемент определяется восемью узлами, толщиной слоев, углом направления свойств материала (направлением системы координат материала) и свойствами ортотропного материала. Промежуточные узлы элемента не могут быть удалены. Треугольный элемент может быть создан путем указания одних и тех же координат для узлов К, L и О.

При создании модели с числом слоев, меньшим трех, элемент SHELL91 более эффективен, чем SHELL99.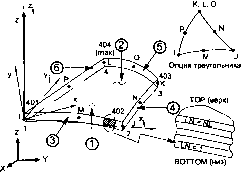

Локальная (местная) система координат для каждого слоя является правой, ось X может быть повернута на угол ТНЕТА (в градусах, указывается в качестве геометрической характеристики) по отношению к оси X системы координат элемента в направлении оси Y элементной системы координат.

Общее число слоев (не свыше 100) должно указываться (посредством NL). Если свойства слоев симметричны относительно срединной поверхности элемента (LSYM = 1), указываются свойства только половины слоев, включая средний (если таковой имеется). В противном случае (LSYM = 0) требуется указывать свойства всех слоев.

Значение ADMSUA является присоединенной на единицу площади массой.

Свойства материала могут быть ортотропными относительно плоскости элемента. Геометрическая характеристика МАТ используется для назначения номера материала вместо номера материала, назначаемого командой МАТ. По умолчанию, если не указывается, геометрическая характеристика МАТ имеет значение 1. Ось X свойств материала соответствует локальному направлению системы координат слоя X.

Для присвоения значений ссылочных температур и демпфирования используются команды TREF и BETAD соответственно. Альтернативой является использование команд MAT.REFT для указания ссылочной температуры или MAT.DAMP для демпфирования; номера материалов слоев в этом случае игнорируются.

Каждый слой элемента многослойной оболочки может иметь переменную толщину (ТК). Толщина считается билинейно изменяющейся по поверхности элемента и указывается в четырех угловых узлах. Если слой имеет постоянную толщину, требуется указывать только значение ТК(1). Если толщина не является постоянной, ее значения указываются во всех четырех угловых узлах. При наличии нелинейных свойств материала толщина слоя не должна превышать трети полной толщины элемента. Общая толщина каждого конечного элемента оболочки должна быть меньше удвоенного радиуса крутки оболочки и меньше одной пятой радиуса кривизны оболочки.

При использовании опции трехслойной оболочки (KEYOPT(9) = 1) элемент использует свойства трехслойной оболочки. Эти свойства специально учитывают применение трехслойной оболочки, в которой имеются тонкие наружные пластины (слои) и относительно толстый ослабленный внутренний слой. Предполагается, что внутренний слой воспринимает все поперечные нагрузки, а наружные слои их не воспринимают. С другой стороны, предполагается, что наружные слои воспринимают все (или практически все) изгибные нагрузки. Обе наружные поверхности состоят из равного числа слоев (которых может быть до семи). При использовании опции трехслойной оболочки для получения лучших результатов в средней поверхности элемента следует использовать значение признака KEYOPT(5) = 1.

Узлы могут располагаться на верхней, средней или нижней поверхности элемента. Выбор места расположения узлов производится при помощи признака расположения KEYOPT(ll). Данный признак может применяться, например, в случаях, когда моделируемые многослойные конструкции имеют расположе-